2 Участок z [0; l]

Такие же действия, как для первого участка, приведут к следующим результатам:

.

.

Получена линейная функция. Поэтому эпюра будет прямолинейной. Достаточно найти две её точки.

N(0) = –16 кH.

Знак минус означает, что избранное направление стрелки не соответствует действительному, т.е. здесь сила направлена влево, к сечению, на сжатие.

N(l)= –16 + 24·1 = 8 кH.

По полученным двум числам строим эпюру продольной силы для данного участка в виде прямой наклонной линии.

Найдём нормальные напряжения. В общем виде имеем линейную функцию

Определим её значения в двух точках. На левом конце участка

На правом конце

Соответствующие относительные деформации

3 Участок z [0; l]

З десь целесообразно рассматривать правую отсечённую часть. Ось z-ов направляем произвольно, вправо. Продольную силу N изображаем в виде стрелки, направленной влево, в положительную сторону, т.е. на растяжение.

Знак плюс, полученный здесь, означает, что продольная сила по направлению совпадает с показанным на рисунке, т.е. направлена от сечения, налево, на растяжение.

Получен результат в виде постоянной величины. Поэтому на эпюре будет горизонтальная линия, отложенная от нулевой в том же масштабе, как для предыдущих участков.

Нормальные напряжения в поперечном сечении:

Относительные деформации:

4 Участок

Составляем уравнение равновесия и находим про­дольную силу:

Нормальные напряжения:

Соответствующие относительные деформации:

Перейдём к определению перемещений. С этой целью по длине стержня намечаем характерные точки a, b, c, e, f, для которых будем вычислять перемещения.

Они совпадают с границами участков. На втором участке действует распределённая нагрузка. Здесь эпюра перемещений будет криволинейной. Поэтому для её построения нужна ещё одна дополнительная точка. В качестве таковой изберём точку d, где N, , равны нулю. Перемещение в этой точке экстремальное (max или min) для этого участка. Найдём её положение, приравнивая продольную силу к нулю

Отсюда имеем

Теперь можно приступить к непосредственному определению перемещений точек. Точка а закреплена, неподвижна. Поэтому

Перемещение точки b равно удлинению четвёртого участка стержня, т.е.

Перемещение точки c равно сумме деформаций третьего и четвёртого участков

Перемещение u_b уже найдено, поэтому

Перемещение точки d равно сумме

где – удлинение участка cd. На этом участке относительная деформация – переменная величина, поэтому его удлинение равно площади треугольника на эпюре т.е.

Таким образом,

Аналогично определяются перемещения точек e и f:

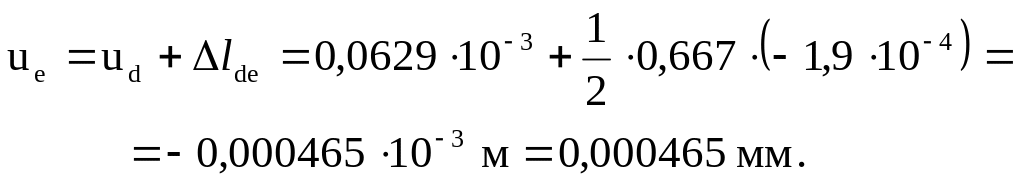
Прочность конструкции проверяем по первой группе предельных состояний. Условие прочности имеет вид

Максимальное по модулю значение нормального напряжения в сечениях стержня, равное 80 МПа, вычислено по нормативным нагрузкам. Его расчётное значение должно быть определено с учётом коэффициента надёжности по нагрузкам, т.е.

.

Следовательно, условие прочности выполняется. Вывод: прочность конструкции обеспечена.