Варианты заданий

Второе число шифра	l м	F1 кН	F2 кН	М1 кНм	М2 кНм	R МПа
1	1,1	22	28	20	24	260	0,80
2	1,0	24	27	21	30	250	0,95
3	1,3	26	25	30	21	270	0,90
4	1,2	30	21	24	26	290	0,85
5	1,1	25	26	23	28	280	0,90

Задача № 13 Внецентренное сжатие короткого стержня

Короткий бетонный столб, поперечное сечение которого задано, сжимается силой F, приложенной в одной из точек В, С, D, E.

Требуется:

1. Вычислить наибольшие растягивающие и сжимающие напряжения в поперечном сечении, выразив их через величину сжимающей силы F.

2. Из условия прочности бруса найти допускаемую нагрузку [F] при заданных расчётных сопротивлениях бетона на растяжение R_р и сжатие R_с.

3. Построить эпюру нормальных напряжений.

4. Построить ядро сечения.

Исходные данные

Шифр	Точка приложения силы	Rр МПа	Rс МПа
31–5	B	1,4	3,1	0,95

Поперечное сечение Решение

Рис. 1

Заданы расчётные сопротивления бетона на растяжение и сжатие и геометрические размеры бруса. Необходимо определить грузоподъёмность, т.е. установить максимальное расчётное значение нагрузки. Для его вычисления воспользуемся условиями прочности бруса из хрупкого материала, имеющего разные расчётные сопротивления на растяжение (R_р) и сжатие (R_c).

(1)

(2)

Рис. 2

Определим геометрические характеристики сечения, необходимые для расчётов. Данное сечение состоит из двух элементов: полукруга и прямоугольника (рис. 1). На более крупном рисунке (рис. 2) обозначим их номерами 1 и 2, наметим центры тяжести для каждого соответственно: C₁, C₂. Проведём через них координатные оси, собственные для каждого элемента и обозначим их: y₁, x, y₂. Ввиду симметричности фигуры, горизонтальные центральные оси обоих элементов совпадают и такая общая ось является центральной для всего сечения. По этой причине введена только одна ось х-ов. Нанесём на чертёж основные размеры.

Поскольку центр тяжести сечения лежит на оси х-ов, нет необходимости в отыскании его координаты y_С. Для вычисления второй координаты x_C проведём вспомогательную ось y₀.

Предварительно определим геометрические характеристики для каждого элемента, необходимые для последующих вычислений.

1. Полукруг. Площадь сечения

,

координата центра тяжести С₁ в системе осей ху₀

х₁ = 20 – 0,424r = 20 – 0,424·20 = 11,52 см.

Осевые моменты инерции

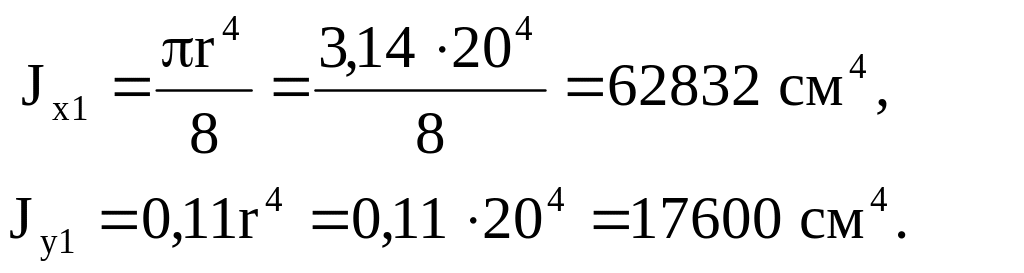
2. Прямоугольник. При аналогичных обозначениях

Общая площадь сечения

A = A₁ + A₂ = 628 + 420 = 1048 см².

Координата центра тяжести сечения

По этим значениям на рис. 2 намечаем точку С и через неё проводим центральную ось у. Ввиду того, что ось х-ов является осью симметрии, оси х, у являются главными осями инерции.

Расстояния между параллельными вертикальными осями х – х₁, х – х₂

Главные осевые моменты инерции относительно центральных осей

Квадраты главных центральных радиусов инерции определяются по формулам

Координаты точки приложения силы совпадают с координатами точки В

Рис. 3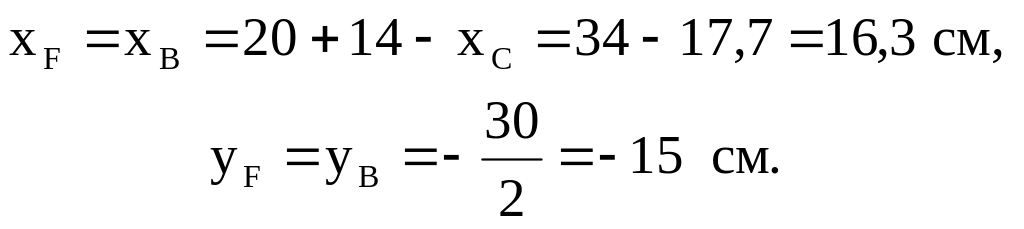

Положение нулевой линии определим с помощью отрезков, отсекаемых ею на координатных осях

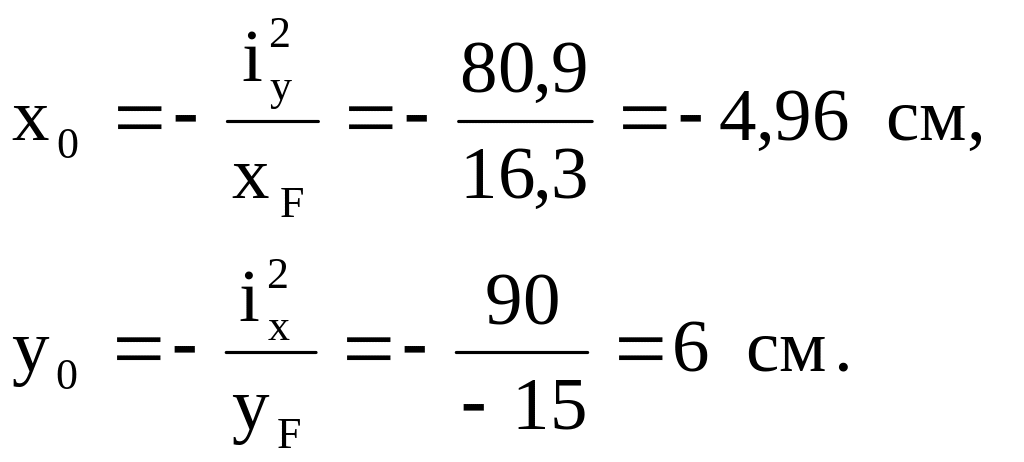
Эти отрезки откладываются на координатных осях и проводится нулевая линия (рис. 3). Её угловой коэффициент равен

k = tg = –y₀/х₀ = –6/(–5) = 1,2, .

Уравнение нулевой линии имеет вид

у = 1,2х + 6.

Для построения эпюры нормальных напряжений необходимо определить точки, наиболее удалённые от нулевой линии, и вычислить напряжения в них. С этой целью проведём линии, касательные к контуру сечения и параллельные нулевой линии. Искомыми точками являются B и D. Прямая OD перпендикулярна нулевой линии и проходит через центр окружности.

Координаты точки B уже определены, координаты точки D найдём по чертежу

x_D = – (20·sin – 2,3) = –13,1 см,

y_D = 20·cos = 12,8 см.

Нормальные напряжения в точках В и D будут

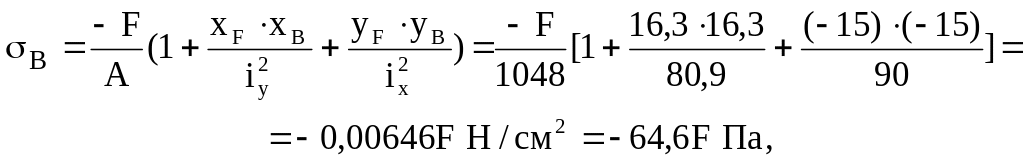⁽⁵⁾

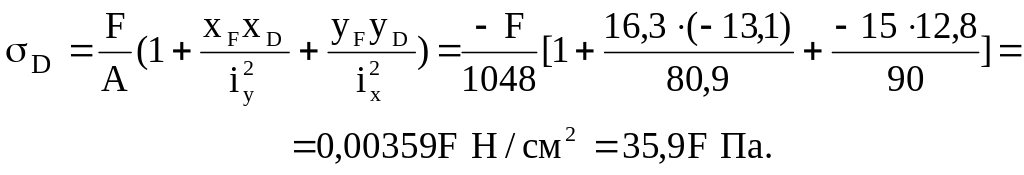⁽⁶⁾

Знак минус перед F в формуле учитывает, что внецентренно приложенная сила является сжимающей. В точке В получено сжимающее, а в точке D – растягивающее напряжения, что соответствует условиям задачи.

Условие прочности по растягивающим напряжениям (1) даёт значение силы

Проведём аналогичные вычисления по сжимающим напряжениям по условию (2)

Меньшее из двух значений силы является грузоподъёмностью или несущей способностью балки

[F] = F₁ = 37 кН.

Подставим полученное значение силы в формулы (5), (6) и получим

Соответствующая эпюра напряжений показана на рис. 3.

Строим ядро сечения. Для этого выбираем достаточное количество положений нулевой линии (с учётом симметрии сечения стойки), которые располагаем по касательным к контуру. В рассматриваемом примере имеется пять таких положений, показанных на чертеже. Каждому положению нулевой линии соответствует конкретная точка приложения силы (x_F, y_F), в то же время являющаяся точкой границы ядра сечения. Определим их координаты.

1. Нулевая линия 1 – 1. Она отсекает на координатных осях отрезки с длинами

x₀ = –x_C = –17,7 см, y₀ = .

Точка приложения силы имеет координаты

На рис. 4 она обозначена как точка 1.

2. Нулевая линия 2 – 2

Этой нулевой линии соответствует точка контура ядра сечения 2.

3. Нулевая линия 3 – 3.

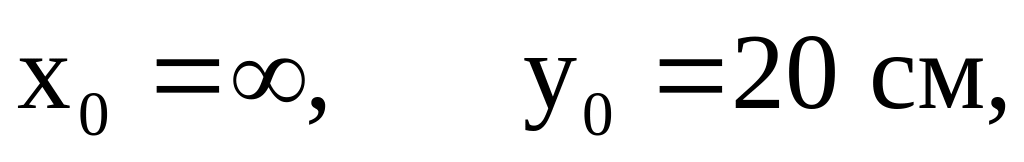
Этой линии соответствует точка 3.

4. Нулевая линия 4 – 4 является прямой, проходящей через две заданные точки G(2,3; 20) и H(16,3; 15). Она описывается соответствующим уравнением

(7)

Поочерёдно приравнивая одну из координат к нулю, найдём координаты, отсекаемые на осях

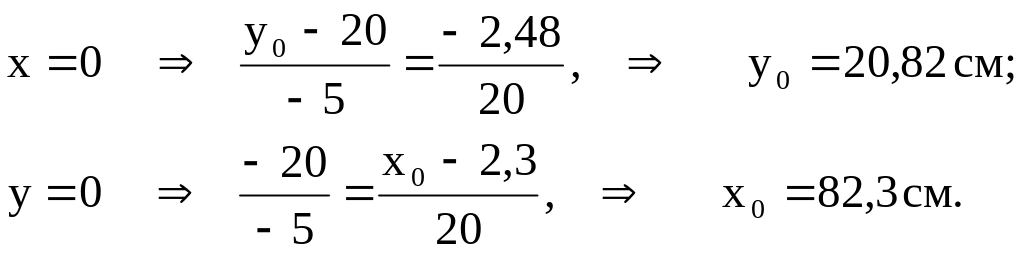
Этой линии соответствует точка 4.

5

Рис. 4

) Нулевая линия 5 – 5, x₀ = 16,3 см, y₀ = .

Этой линии соответствует точка 5.

Изображаем полученные точки и соединяем их линиями (рис. 4). Если при переходе от одного положения нулевой линии к соседнему положению она поворачивается вокруг одной точки (например, от 3 – 3 к 4 – 4), то линия перемещения силы (т.е. граница ядра сечения) есть прямая (через точки 3 и 4). В остальных случаях (например, поворот от 1 – 1 к 2 – 2 и далее к 3 – 3) сила перемещается по кривой границе ядра сечения (1–2–3). Другую половину ядра сечения строим, используя его свойство симметрии (точки 2^', 3^', 4^').