2.5. Відношення порядку

Бінарне відношення α на множині X називається відношенням порядку, якщо воно транзитивне:

та антисиметричне:

Приклад1. Розглянемо відношення "старше" на множині людей. Очевидно, що воно транзитивне та антисиметричне, отже, воно є відношенням порядку.

Множина X з визначеною на ній відношенням порядку α називається впорядкованою множиною та позначається < X, α>.

Відношення порядку α називається відношенням нестрогого порядку на множині X, якщо α рефлексивне:

Відношення нестрого порядку позначається символом « ≤ ». Якщо х ≤ у, то говорять, що "елемент x передує елементу y" або "y слідує за x".

Приклад 2. Відношення х ≤ у на множині дійсних чисел є відношенням нестрогого порядку.

Приклад 3 На сукупності підмножин деякої універсальної множини U відношення А  В є відношенням нестрогого порядку.

Приклад 4. Відношення m/n (m ділить n) на довільній підмножині натуральних чисел {2, 3, 6, 7, 14} є нестрогим порядком.

Два елементи x, y  X називаються порівнювальними елементами впорядкованої множини X, якщо або х α у, або у α х.

Не порівнювальними елементами у впорядкованій множині {2, 3, 6, 7, 14} є , наприклад, елементи 7 та 2, 2 та 3, 3 та 7.

Відношення порядку називається відношенням строгого порядку на множині X, якщо α антирефлексивне:

.

Відношення строгого порядку позначається символом « < ».

Приклад 5. Нехай f и g – функції з однаковими областями визначення. Визначмо відношення « > » наступним образом: f > g, якщо для будь-якого x з області визначення функції f(x) > g(x). Очевидно, що дане відношення є відношенням строгого порядку.

Для функцій f и g, зображених на рисунку 10, має місце співвідношення f > g. Пари функцій f та h, а також g та h є непорівнювальними.

Рис. 10

Приклад 6. Алфавітний порядок є відношенням строгого порядку на множині букв.

Нехай на множині X задано відношення строгого порядку « < ». Елемент такий, що для будь-якого y з X, який не співпадає з x, виконується відношення x < y (x > y) називається найменшим (найбільшим).

Нехай на множині X задано відношення строго порядку « < ». Тоді елемент x Î X називається мінімальним (максимальним) в упорядкованій множині < X, < >, якщо не існує ніякого елемента y, для якого y < x (відповідно y > x).

2.6. Функції і відображення

Бінарне відношення R між множинами А та В називається функцією, якщо з aRb та aRc слідує, що b =c; тому для будь-яких х Î А існує один у Î В такий, що хRу або R(х)={y}.

Зауважимо, що якщо R(х) існує (тобто R(х)≠ ), то цей елемент єдиний і записують у=R(х).

Функції позначають маленькими латинськими літерами f, g, h, …Якщо f – функція між множинами А та В, то цей факт записують так: f: А → В. Отже, якщо х Î А і х f у, то будемо позначати відношення наступним чином f: х → у.

Приклад 1. Функція f: А → А, де А= {-1, 0, 1} визначається відношенням f: х → х³.

Функція f: А → В є відображенням, якщо її область визначення співпадає з А.

Функції, які не є відображеннями, називають частковими.

Відображення на множину називається перетворенням.

Зразки розв’язання типових завдань

1. Для множин X = { 1, 5, 8 } та Y = { 2, 3, 6 } скласти бінарні відповідності P₁, P₂, які задовольняють наступним умовам:

P₁= { ( x, y ) / x < y , x  X і y  Y }

P₂= { ( x, y ) / x y ≥ 30 , x  X і y  Y }.

1. Побудувати 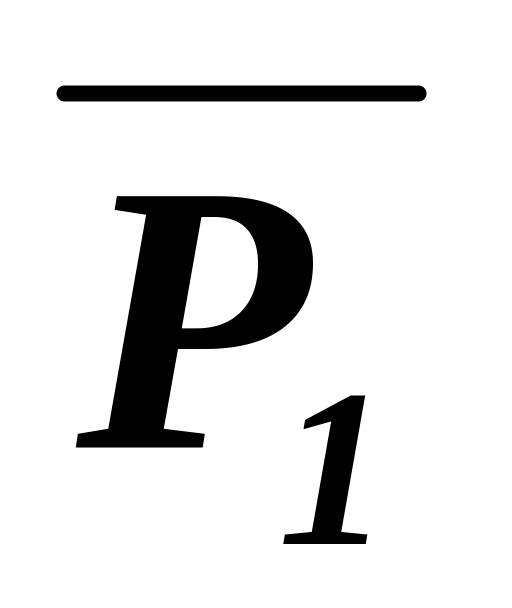, P₁  Р₂, P₁  Р₂, P₁\ P₂, Р₂\ P₁, Р₁  Р₂.

2. Знайти:

а) проекції Pr₁(P₁) та Pr₂(P₁);

б) розтини S_l ( 5, P₂) та Sr ( P₂, 6);

в) інверсії P₁^-1 та P₂^-1;

г) композиції R₁ = P₁ ○ Q та R₂ = P₂ ○ Q, де Q  Y ´ Z і Z = {k, m}.

P₁ = { ( 1, 2 ), ( 1, 3 ), ( 1, 6 ), ( 5, 6 ) }

P₂= { ( 5, 6 ), ( 8, 6 ) }

1) = { ( 5, 2 ), ( 5, 3 ), ( 8, 2 ), ( 8, 3 ), ( 8, 6 ) }

P₁  Р₂= { ( 1, 2 ), ( 1, 3 ), ( 1, 6 ), ( 5, 6 ), ( 8, 2 ), ( 8, 3 ), ( 8, 6 ) }

P₁  Р₂= { ( 5, 6 ) }

P₁\ P₂= { ( 1, 2 ), ( 1, 3 ), ( 1, 6 ) }

Р₂\ P₁= { ( 8, 2 ), ( 8, 3 ), ( 8, 6 ) }

Р₁  Р₂= ( P₁\ P₂ ) (Р₂\ P₁)= { ( 1, 2 ), ( 1, 3 ), ( 1, 6 ), ( 8, 2 ), ( 8, 3 ), ( 8, 6 ) }

2) а) Pr₁(P₁)= { 1, 5 }, Pr₂(P₁)= { 2, 3, 6 }.

б) S_l ( 5, P₂)= { 6 }, Sr ( P₂, 6 )= { 5, 8 }.

в) P₁^-1= { ( 2, 1 ), ( 3, 1 ), ( 6, 1 ), ( 6, 5 ) }, P₂^-1= { ( 6, 5 ), ( 2, 8 ), ( 3, 8 ), ( 6, 8 ) }.

г) Q = { ( 2, k ), ( 2, m ), ( 3, k ), ( 3, m ), ( 6, k ), ( 6, m ) }

R₁ = P₁ ○ Q = { ( 1, k ), ( 1, m ), ( 5, k ), ( 5, m ) }

R₂ = P₂ ○ Q = { ( 5, k ), ( 5, m ), ( 8, k ), ( 8, m ) }

2. Для множини А = {1, 2, 3} скласти бінарні відношення P, щоб вони володіли властивостями рефлексивності, симетричності, транзитивності.

P = { ( 1, 1), ( 2, 2 ), ( 3, 3) } – рефлективність виконується

P = { ( 3, 1 ), ( 1, 3 ), ( 1, 2 ), ( 2, 1 ), ( 1, 1 ), ( 2, 2 ), ( 3, 3 ) } – симетричність виконується

P = { ( 1, 1), ( 1, 3 ), ( 3, 2), ( 2, 3 ) ( 1, 2), ( 2, 1 ), ( 3, 3 ) } – транзитивність виконується

3. Визначити, чи є еквівалентністю бінарне відношення P на множині A. Для відношення, що не є еквівалентністю, вказати, які з властивостей – рефлексивність, симетричність, транзитивність – порушуються.

P = { ( x, y ) / x, y  N, х – дільник у }

Бінарне відношення P:

1. рефлексивне, оскільки х / х =1 для всіх N;

2. несиметричне, оскільки 2 – дільник 4, але 4 не є дільником 2;

3. транзитивне, оскільки якщо y /x  N та z /y  N, z/x = (y /x) * (z /y)  N.

4. антисиметричне, оскільки якщо х /у  N та y /x  N , то х = у.

Варіанти індивідуальних завдань

Завдання 1. Для множин A = { x  x N, -3 ≤ x ≤ 3} та B = { x  x N, -6 ≤ x ≤ 6} скласти бінарну відповідність Р₁, яка задовольняє умовам:

1. P₁= { ( x, y ) / x, y  A ´ B, у/х}, де у/х – ділення без остачі

2. P₁= { ( x, y ) / x, y  A ´ B, х+у ≤ 0}

3. P₁= { ( x, y ) / x, y  A ´ B, 2х ≥ 3у}

4. P₁= { ( x, y ) / x, y  A ´ B, ху ≤ 0}

5. P₁= { ( x, y ) / x, y  A ´ B, х ≥ у}

6. P₁= { ( x, y ) / x, y  A ´ B, (х-у)/3}

7. P₁= { ( x, y ) / x, y  A ´ B, |х-у|≤3}

8. P₁= { ( x, y ) / x, y  A ´ B, х, у – парні числа}

9. P₁= { ( x, y ) / x, y  A ´ B, х, у – непарні числа}

10. P₁= { ( x, y ) / x, y  A ´ B, х / у}, де х / у – ділення без остачі

11. P₁= { ( x, y ) / x, y  A ´ B, |х|=|у|}

12. P₁= { ( x, y ) / x, y  A ´ B, (х, у)=1}, (х, у)=1­ – числа х, у є взаємно простими

13. P₁= { ( x, y ) / x, y  A ´ B, |х| < у}

14. P₁= { ( x, y ) / x, y  A ´ B, х ≤ у}

15. P₁= { ( x, y ) / x, y  A ´ B, (х - у) – парне число}

16. P₁= { ( x, y ) / x, y  A ´ B, (х + у) – парне число}

17. P₁= { ( x, y ) / x, y  A ´ B, х² = у}

18. P₁= { ( x, y ) / x, y  A ´ B, х + у =0}

19. P₁= { ( x, y ) / x, y  A ´ B, 2х+3 = у}

20. P₁= { ( x, y ) / x, y  A ´ B, х-у =0}

Завдання 2. Для бінарних відповідностей P₁ ( див. завдання 1) та P₂= { ( x, y ) / -1 ≤ x ≤ 1, 0 ≤ у ≤ 3x, y  Z} побудувати , P₁  Р₂, P₁  Р₂, P₁\ P₂, Р₂\ P₁, Р₁  Р₂.

Завдання 3. Для бінарних відповідностей P₁ та P₂, побудованих в завданнях 1-2, знайти:

а) проекції Pr₁(P₁) та Pr₂(P₁);

б) інверсії P₁^-1 та (P₁  Р₂)^-1;

в) композиції R₁ = P₁ ○ Q та R₂ = P₂ ○ Q, де Q  С ´ D і C = { -2, -1, 0, 1},

D = {3, 4, 5}.

Завдання 4. Вказати, які з властивостей – рефлексивність, симетричність, антисиметричність, транзитивність – має відношення R на множині A, де:

1. A={1, 2, 3, 4}, R={(1,1), (2,2), (3,3), (4,4), (1,2), (2,3), (2,1), (3,2), (1,3), (3,1)};

2. A={1, 2, 3, 4}, R={(1,1), (2,2), (3,3), (4,4), (1,2), (2,1), (3,4), (4,3)};

3. A={1, 2, 3, 4}, R={(1,1), (2,2), (3,3), (4,4), (2,3), (2,4), (3,2), (4,2), (3,4), (4,3)};

4. A={1, 2, 3, 4}, R={(1,1), (2,2), (3,3), (4,4), (1,2), (1,3), (1,4)};

5. A={1, 2, 3, 4}, R={(1,1), (2,2), (3,3), (4,4), (1,2)};

6. A={1, 2, 3, 4}, R={(1,1), (2,2), (3,3), (4,4), (1,2), (2,3), (4,1), (1,4)};

7. A={1, 2, 3, 4}, R={(1,1), (2,2), (3,3), (1,2), (2,1), (1,3)};

8. A={1, 2, 3, 4}, R={(1,1), (2,2), (3,3), (1,2), (2,3), (3,1)};

9. A={1, 2, 3, 4}, R={(1,1), (2,2), (3,3), (1,2), (2,3), (1,3), (3,2)};

10. A={1, 2, 3}, R={(1,1), (2,2), (3,3), (1,2), (2,1)};

11. A={1, 2, 3}, R={(1,1), (2,2), (3,3), (1,2), (2,3), (1,3)};

12. A={1, 2, 3}, R={(1,1), (2,2), (3,3), (1,3), (3,1)};

13. A={1, 2, 3}, R={(1,1), (2,2), (3,3), (1,3), (3,2)};

14. A={1, 2, 3}, R={(1,1), (2,2), (3,3)};

15. A={1, 2, 3}, R={(1,1), (2,2), (3,3), (1,2)};

16. A={1, 2, 3}, R={(1,1), (2,2), (1,2), (2,1)};

17. A={1, 2, 3}, R={(1,1), (3,3), (1,2), (2,3)};

18. A={1, 2, 3}, R={(1,1), (2,2), (3,3), (1,2), (2,1), (2,3)};

19. A={1, 2, 3, 4, 5}, R={(1,2), (1,3), (1,4), (2,5), (3,5), (4,5)};

20. A={1, 2, 3, 4, 5, 6}, R={(1,2), (1,3), (3,4), (3,5), (4,6), (5,6)};

Завдання 5. Визначити, чи є еквівалентністю відношення R на множині A. Для відношення, що не є еквівалентністю, вказати, які з властивостей – рефлексивність, симетричність, транзитивність – порушуються.

1. R = { ( x, y ) / x, y  N, х у}

2. R = { ( x, y ) / x, y  N \ {1}, х та у мають спільний дільник}

3. R = { ( x, y ) / x, y  N, (х - у) – парне число}

4. R = { ( x, y ) / x, y  N, (х + у) – парне число}

5. R = { ( x, y ) / x, y  N, х < у}

6. R = { ( x, y ) / x, y Î N, у-1< х <у+2}

7. R = { ( x, y ) / x, y Î N, х² ≤ у}

8. R – відношення паралельності на множині прямих площини

9. R – відношення перпендикулярності на множині прямих площини

10. R – відношення рівності на множині дійсних чисел (R)

11. R – відношення «<» (менше) на множині дійсних чисел (R)

12. R – відношення «≤» (менше або рівно) дійсних чисел (R)

13. R – відношення перетину на множині прямих площини

14. R = { ( x, y ) / x, y  Z⁺, | х – у |≤3}

15. R = { ( x, y ) / x, y  Z⁺, х, у – парні числа}

16. R = { ( x, y ) / x, y  Z⁺, |х|=|у|}

17. R = { ( x, y ) / x, y  Z⁺, (х, у)=1}, (х, у)=1­ – числа х, у є взаємно простими

18. R = { ( x, y ) / x, y  Z⁺, |х| > у}

19. R – відношення концентричності на множині кіл на площині

20. R – відношення подібності на множині трикутників на площині

8