2. Бінарні відповідності і відношення

2.1. Основні поняття

Будь-яка підмножина P декартового добутку множин A і B називається бінарною відповідністю з множини A в множину B (P  A  B) При цьому множина A називається множиною відправлення, а множина B - множиною прибуття відповідності P.

Будь-яка підмножина P декартового квадрата A² називається бінарним відношенням на множині A (P  A²).

Якщо впорядкована пара α = (a, b) належить деякому відношенню Р, то кажуть, що а знаходиться у відношенні Р до b та записують a Р b.

Відношення, що складається з пар (b, a), отриманих перестановкою членів даного відношення Р пар (a, b), називається оберненим до Р та позначається Р^-1 .

Наприклад. Для множин X = { 1, 5, 8 } и Y = { 2, 3, 6 } скласти бінарну відповідність P = { ( x, y ) | x < y , x  X і y  Y } .

1) Відповідність P = { ( 1, 2 ), ( 1, 3 ), ( 1, 6 ), ( 5, 6 ) }.

2) Граф відповідності:

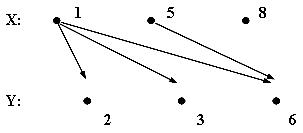
Рис.1.

3) Обернена відповідність = { ( 2, 1 ), ( 3, 1 ), ( 6, 1 ),( 6, 5 ) }.

2.2. Операції над бінарними відповідностями і відношеннями

Бінарні відповідності і відношення є частинними випадками множин, отже, для них аналогічно ввояться теоретико-множинні операції, зокрема, об’єднання, перетин, різниця та доповнення. Крім того, існують специфічні операції над бінарними відповідностями і відношеннями: проекція, розтин, інверсія і композиція.

Проекція

Операція, яка кожній парі α = (a, b) з декартового добутку A ´ B ставить у відповідність її першу (другу) координату, називається проекцією пари  на першу (другу) координатну вісь. Операція позначається:

Pr₁ (α )=a – проекція пари α на першу координатну вісь

Pr₂(α )=b – проекція пари α на другу координатну вісь

Проекції Pr₁(P) і Pr₂(P) відповідності P  A ´ B на першу і другу координатні вісі визначаються як підмножини множин A і B, відповідно:

Pr₁(P)={ a / a=Pr₁ (α ) для всіх α  P}

Pr₂(P)={ b / b=Pr₁ (α ) для всіх α  P}

Розтин

Лівим розтином елемента a  A в відповідності P  A ´ B називається множина, яка скдадається з елементів b  В заданої відповідності і позначається:

S_l ( a, P) ={ b / b  B, (a, b)  P }.

Правим розтином елемента b  B в відповідності P  A ´ B називається множина, яка складається з елементів a  A заданої відповідності і позначається:

Sr ( P, b)={ a / a  A , (a, b)  P }.

Інверсія

Пара α^-1=(b, a)  B ´ A називається інверсною по відношенню до пари α= (a, b)  A ´ B. Операція співставлення парам α їх інверсних пар α^-1 називається інверсією.

Якщо P - відповідність із A в B, то під інверсною відповідністю P^-1 розуміють відповідність із B в A, яка складається з пар, інверсних парам відповідності P і позначається:

P^-1 = { (b, a) / a  A; b  B ; (a, b)  P }.

Композиція

Нехай задано відповідність P  A ´ B і відповідність Q  B ´ C. Композицією називається відповідність R  A´ C, яка складається з пар, у яких перший елемент a  A і другий елемент с  С, при умові, що існує таке b  B, що a, b)  P і (b, c)  Q і позначається:

R = P ○ Q = { (a, c) /  b  B: (a, b)  P, (b, c)  Q}.