Вопрос 2

Коэффициент Пуассона. При всем многообразии случаев произвольную деформацию тела можно свести к двум элементарным деформациям — растяжению (сжатию) и сдвигу. При растяжении резинового шнура его поперечный размер d уменьшается до величины d₁. Такое поперечное сжатие характеризуется параметром _=(d₁–d)/d=d/d. Продольный размер изменяется на l и характеризуется величиной =(l₁–l)/l=l/l. Опытным путем установлено, что отношение _ к  приблизительно одинаково для разных деформаций одного и того же материала. Поэтому в теории упругости материал характеризуется коэффициентом Пуассона:

=–(_/)

Подсчитаем численное значение коэффициента Пуассона. Чтобы ответить на этот вопрос, подсчитаем изменение объема резинового шнура:

V=ld², V₁=l₁d₁²=l(1+)d²(1+_)²= [раскроем скобки и пренебрежём _², 2_, _²] V(1++2_)

V/V=(V₁–V)/V+2_=(1–2).

Коэфф. всестороннего сжатия (возникает в условиях одинакового давления на все поверхности тела)

V/V= –p/K (p – внешнее давление)

К=Е / 3(1–2)

при ₁=₂=₃=: V/V = (3 /E)* (1–2).

Законы Гука. В ряде практически важных случаев напряжения определяются только деформациями. Такие тела называются абсолютно упругими, или упругими. Замечательным свойством таких тел является способность полностью восстанавливать свою форму после снятия внешних усилий, прикладываемых к телу. Рассмотрим, например, растяжение (или сжатие) стержня под действием силы F, приложенной перпендикулярно к торцевой грани с площадью сечения S. При последовательном возрастании нагрузки вначале деформации развиваются равномерно по длине стержня и растут пропорционально нагрузке: =(l₁–l)/l=F/SE=/E. Величина  =F/S называется нормальным напряжением в торцевом сечении стержня. Пропорциональность деформаций  соответствующим напряжениям выражает закон Гука. Е – модуль Юнга. Закон Гука окончательно записывают в виде =/Е.

Опыт показывает, что этот закон выполняется лишь в определенном интервале напряжений. При некотором напряжении появляется заметное остаточное удлинение. Это напряжение s называется пределом упругости. Закон Гука выполняется только в части области упругости — области пропорциональности. При возрастании нагрузки наблюдается явление текучести, т.е. рост удлинения образца при постоянной нагрузке , называемой пределом текучести. Отметим, что течение материала происходит равномерно по всей длине стержня. За пределами области текучести дальнейшее удлинение стержня сопровождается увеличением . Однако деформации будут распределены уже неодинаково по длине стержня — в некотором месте можно заметить образование шейки. При напряжении M , называемом пределом прочности, в этом ослабленном сечении происходит разрыв. Аналогичными обладают и деформации сдвига. В области пропорциональности связь между деформацией и касательным напряжением задаётся соотношением: =F/(GS)=_/G, где _=F/S – касательное напряжение, а G – модуль сдвига.

У становим зависимость G от Е. Обратим внимание на то, что квадратная грань ABCD параллелепипеда (рис. 1.9), находящегося внутри рассматриваемого кубика, превращается при деформации в ромбическую грань A’B’C’D’. Совершенно ясно, что параллелепипед испытывает сдвиговую деформацию, а его объем при этом практически не изменяется. Величину угла сдвига  можно легко связать с деформацией удлинения =l/l и коэффициентом Пуассона =–_/. Из треугольника A'OD’ следует, что:

П оскольку b <<1, то

В последней формуле учтено, что e << 1. Сила F, растягивающая кубик (рис. 1.10), создает нормальное напряжение =F/l². Это напряжение передается на грани AB и BC параллелепипеда, однако силы, действующие на каждую из граней, имеют не только нормальную к грани, но и направленную вдоль грани составляющую F_. Касательное напряжение оказывается при этом равным: 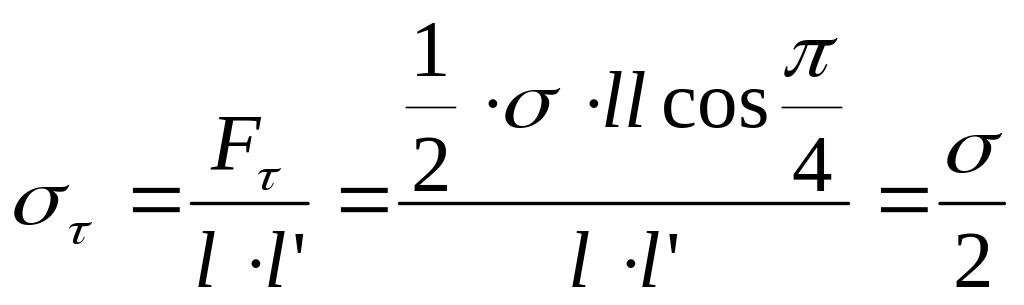(1.24)

Поскольку деформации e в формуле (1.23) пропорциональны напряжениям, а =2_, то: =2(1+)_/E. Сравнивая последнее равенство с соотношением =F/(GS)=_/G и учитывая, что =tg, получаем то, что искали: G = E /2(1+).

Модуль Юнга, коэффициент Пуассона. Модуль сдвига. Энергия деформированного тела.

Для стержней:  E , где  - напряжение на торце стержня F/S, где F – продольная сила действующая на торец стержня, S – площадь поперечного сечения стержня E – модуль Юнга – характеристика материала из которого сделано тело. l/l₀, где l изменение длины стержня, а l₀ - начальная длина стержня.

Коэфф. Пуассона μ ≡ - (Δd/d)/( Δl/l) = - (λ_y/λ_x)= - (λ_z/λ_x) (при растяжении или сжатии вдоль оси x)

μ _max=1/2

Сдвиг: τ=Gγ, где τ-касательное напряжение на поверхности бруска τF/S где F – касательная сила действующая на поверхность пластины, S – площадь этой поверхности, γ – малый угол наклона боковой грани бруска, а G – модуль сдвига, характеризующий упругие свойства материала.

Энергия деформированного стержня W=kx²/2.