Билет 20 Вопрос 1

Собственная длина и собственное время. Лоренцево сокращение длины. Релятивистское замедление хода часов.

Вопрос 2

Связанные системы. Нормальные колебания (моды). Нормальные частоты.

Нормальными называются такие колебания системы, при которых все части её колеблются по гармоническому закону с одинаковой частотой.

Если система обладает несколькими степенями свободы, то при малых отклонениях от положения равновесия возможны колебания сразу по всем степеням свободы. Обычный маятник может колебаться в двух взаимно перпендикулярных вертикальных плоскостях, проходящих через точку подвеса. Поэтому он имеет две степени свободы. Наличие связи различных степеней свободы между собой придает колебанию системы со многими степенями свободы новые физические закономерности.

Связанной системой называется система со многими степенями свободы, между которыми имеется связи, обеспечивающие возможность обмена энергией между различными степенями свободы. Примером связанной системы с двумя степенями свободы могут служить два маятника, соединенных между собой пружиной.

k

k

k1

пружина

два пружинных маятника

x1

x2

Несмотря на сложность движения двух связанных маятников, оно всегда может быть представлено как суперпозиция четырех гармонических колебаний, частоты которых называются нормальными частотами связанной системы. Число нормальных частот равно числу степеней свободы. В приведенном примере имеем две степени свободы. И можно представить колебание как суперпозицию двух колебаний.

ωI S^I₁(t)=S20sin(ω_I*t+φ_I)

S^I₂(t)=S₁₀sin(ω_I*t+φ_I)

ωI, S^I20/S^I10=1 – первая мода

ωI=√(k/m)

ωII S^II₁(t)=S^II20*sin(ω_II*t+φ_II)

S^II₂(t)=S^II_10*sin(ω_II*t+φ_II)

ωII, S^II20 / S^II₁₀ = -1 – вторая мода

ωII=√((k+2k1)/m)

S₁(t)=S^I10*sin(ω_I*t+φ_I)+S^II10*sin(ω_II*t+φ_II)

S₂(t)=S^I20*sin(ω_I*t+φ_I)+S^II20*sin(ω_II*t+φ_II)

ωI,ωII, S^I20/S^I10, S^II20 / S^II₁₀ } известны

Начальные условия S1(0), S1^'(0)

S₂(0), S₂^'(0) } → S^I10 ; φ_I

S^II10 ; φ_II

Если маятинки отклонить одинаково в одну сторону, то они колеблются с некоторой частотой ω1, которая называется нормальной. Частота колебаний маятников, отклоненных одинаково в противоположных направлениях, является другой нормальной частотой ω2.

Если ω_I ≈ ω_II , |ω_I – ω_II | <<ω_I ≈ ω_{II ,} тогда отчетливо будут наблюдаться биения. Биение – колебание, которое происходит с медленной частотой и является суммой двух гармонических колебаний с близкими частотами. Это колебание с изменяющейся амплитудой. Оно лишь приблизительно гармоническое с частотой ω_I ≈ ω_II , а его амплитуда изменяется с частотой |ω_I – ω_II |. T_биен=2/(ω_I – ω_{II ).}

_Δω=ω_I – ω_II

<ω>=(ω_I +ω_II)/2

S₁(t)=2*S₁(t)*(cos( _Δω/2)t) *cos(<ω>t)

S₂(t)=2*S₁(t)*(sin( _Δω/2)t) *cos(<ω>t)

Билет 21

Вопрос 1

Сложение скоростей в релятивистской механике

Вопрос 2

Волны. Распространение «импульса» в среде. Продольные и поперечные волны. Уравнение бегущей волны. Скорость волны и скорости «частиц».

Волна – процесс распространения состояния.

Волновая поверхность – поверхность, во всех точках которой данная физическая величина имеет одно значение в любой момент времени.

Уравнение бегущей волны:

Его решение: y(x,t) = f(t- x/v) + g(t+x/v), где f и g - произвольные дважды дифференцируемые по обеим переменным функции.

Волновое уравнение.

S(t,r)=S₀sin(t– ); ²S/t²=–²S; 

²S/x²+²S/y²+²S/z²=–S(k_x²+ k_y²+k_z²)=–Sk²

²S/(t²c²)=²S/x²+²S/y²+²S/z²

²S/t²=S/c², где S – оператор Лапласа. c=/k

Волновому уравнению также удовлетворяет уравнение любого импульса.

S=S(t– /c)

Вывод волнового уравнения для бегущих волн по струне.

1) Поперечные волны:

Пусть натяжение в струне Т. При малых деформациях изменением натяжения можно пренебречь. Пусть (х) - угол между силой Т и горизонталью, p – линейная плотность струны.

dx T(x+dx)



T(x)

Из закона Ньютона для элемента (x,x+dx):

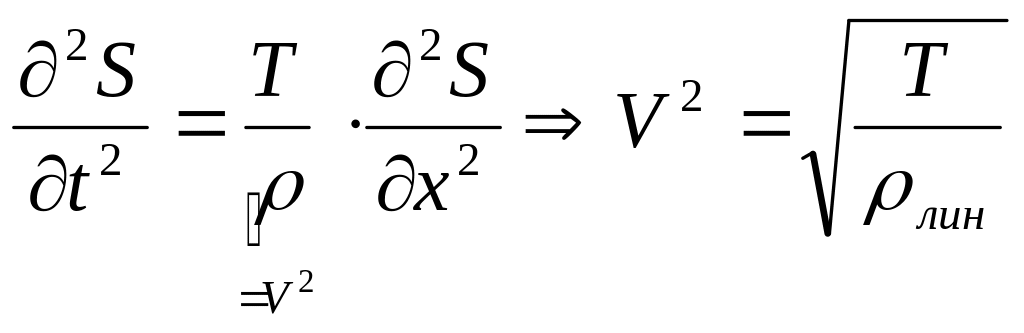dx²S/t²=T(sin_x+dx - sin_x )=T(tg_x+dx – tg_x)=T((x+dx)–(x))=T , где  – линейная плотность,  , S(t,x)=S(t–(x/c)).

2) Продольные волны в твёрдом теле:

(рисунок)

=dx’/dx, (>0 – сжатие, <0 – растяжение).

dm=dx, ( – площадь), dm(²S/t²)=F=F(x+x)–F(x)=E 

mdx(²S/t²)=E  (²S/t²)=(E/)(²S/x²)  c²=E/