Вопрос 2.

Колебания. Число степеней свободы системы. Свободные колебания системы с одной степенью свободы. Уравнение собственных незатухающих колебаний. Его решение.

Колебания – повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия.

?Колебания называются периодическими, если значения физич. величин повторяются через равные промежутки времени.

Колебательный процесс может возникнуть за счёт внешней силы, которая вывела систему из равновесия и перестала действовать, а колебания происходят под действием только внутренних сил, без участия внешних. Такие колебания наз. собственными (колебания системы, предоставленной самой себе).

Числом степеней свободы системы называется количество независимых координат, при помощи которых можно полностью задать положение системы в пространстве.

Колебания с одной степенью свободы – это колебания при которых движения системы можно описать одним независимым параметром (координатой). Пример: колебания математического маятника, колебания физического маятника (твёрдое тело, подвешенное за точку и способное колебаться вокруг оси, не проходящей через ц. м.), колебания груза на пружинке.

Уравнение гармонических незатухающих колебаний: x’’ + ω₀²x=0

Решение уравнения гармонических незатухающих колебаний: x = X₀ sin (ωt+φ).

Уравнения для физического маятника: J=–mgasin–mga, приведённая длина физического маятника, равна длине математического маятника с тем же периодом – l=J₀+ma²/ma. T= , решение этого уравнения: =₀cos(t+), (₀,  определяются начальными условиями,  – параметр системы).

Колебания, происходящие по закону синуса или косинуса наз. гармоническими.

Билет 13 Вопрос 1

Соударение тел. Абсолютно упругий и неупругий удары. Применение законом сохранения для описания столкновения тел.

Абсолютно неупругим ударом, называется столкновение двух тел, в результате которого они соединяются вместе и движутся дальше как одно тело.

Сталкивающиеся тела деформируются, возникают упругие силы и т.д. Однако если удар неупругий то, в конце концов все эти процессы прекращаются, и в дальнейшем оба тела, соединившись вместе, движутся как единое твёрдое тело.

v₁ v₂

m₁ m₂

Рассмотрим абс. неупругий удар на примере столкновения двух шаров. Пусть они движутся вдоль прямой, соединяющей их центры, со скоростями v₁ и v₂. В этом случае говорят что удар является центральным. Обозначим за V общую скорость шаров после соударения. Закон сохр. Импульса даёт:

m₁v₁+m₂v₂=(m₁+m₂)V  V=(m₁v₁+m₂v₂)/(m₁+m₂)

Кин. энергии системы до удара и после: K₁=1/2(m₁v₁²+m₂v₂²), K₂=1/2(m₁+m₂)V

Пользуясь этими выраж. получаем: K₁-K₂=1/2v₁v₂^2

г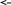 де =m₁m₂/(m₁+m₂) – приведенная масса шаров. Таким образом, при столкновении двух абсолютно неупругих шаров происходит потеря кин. энергии макроскопического движения, равная половине произведения приведённой массы на квадрат относительной скорости.

Абсолютно упругим ударом называется столкновение тел, в результате которого их внутренние энергии не меняются. Пример: Столкновение бильярдных шаров из слоновой кости, при столкновениях атомных, ядерных частиц. Рассмотрим центральный удар двух шаров, движущ-ся навстречу друг другу:

(m₁v₁²)/2+(m₂ v₂²)/2=(m₁u₁²)/2+(m₂ u₂²)/2

и:

m₁v₁+m₂v₂=m₁u₁+m₂u₂

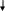
u1=[(m₁-m₂)v₁+2m₂v₂]/(m₁ +m₂)

u2=[(m₂-m₁)v₂+2m₁v₁]/(m₁+m₂)

(При столкновении двух одинаковых абсолютно упругих шаров они просто обмениваются скоростями)