Вариант 6
Задание 1.
Имеются данные по итогам экзаменационной сессии в группе (10 студентов) о зависимости между количеством пропущенных занятий Х (ч) и средним баллом успеваемости по предметам Y:
X |
0 |
6 |
38 |
25 |
20 |
55 |
28 |
34 |
14 |
32 |
Y |
4,8 |
5,0 |
3,8 |
3,7 |
3,5 |
3,0 |
4,1 |
3,9 |
4,6 |
3,9 |
Составить уравнение линейной регрессии y = a + bx + ε, используя МНК, и найти числовые характеристики переменных.
Вычислить коэффициент корреляции, коэффициент детерминации.
Оценить полученное уравнение регрессии.
Найти доверительные интервалы для
и
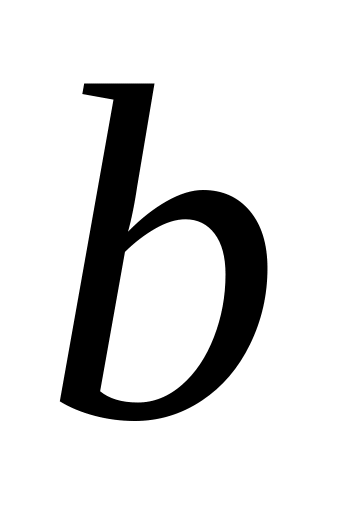при уровне значимости α = 0,05.Вычислить среднюю ошибку аппроксимации и оценить качество выбранного уравнения регрессии.
Решение:
Для расчёта параметров уравнения регрессии построим расчётную таблицу 1.1.
Таблица 1.1.
Расчётная таблица
№ |
х |
у |
х2 |
у2 |
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
0 |
4.8 |
0 |
23.04 |
0 |
4.86 |
-0,06 |
0.003602 |
2 |
6 |
5 |
36 |
25 |
30 |
4.66 |
0,34 |
0.11 |
3 |
38 |
3.8 |
1444 |
14.44 |
144.4 |
3.61 |
0,19 |
0.0367 |
4 |
25 |
3.7 |
625 |
13.69 |
92.5 |
4.04 |
-0,34 |
0.11 |
5 |
20 |
3.5 |
400 |
12.25 |
70 |
4.2 |
-0,7 |
0.49 |
6 |
55 |
3 |
3025 |
9 |
165 |
3.05 |
-0,05 |
0.002349 |
7 |
28 |
4.1 |
784 |
16.81 |
114.8 |
3.94 |
0,16 |
0.0263 |
8 |
34 |
3.9 |
1156 |
15.21 |
132.6 |
3.74 |
-0,74 |
0.0256 |
9 |
14 |
4.6 |
196 |
21.16 |
64.4 |
4.4 |
0,2 |
0.0404 |
10 |
32 |
3.9 |
1024 |
15.21 |
124.8 |
3.81 |
0,09 |
0.008831 |
Итого |
252 |
40.3 |
8690 |
165.81 |
938.5 |
40.3 |
-0,91 |
0.86 |
Для начала рассчитаем параметры уравнения регрессии:
Найдём выборочные средние по х и у.
Выборочные дисперсии:
Среднеквадратическое отклонение
Линейное уравнение регрессии имеет вид y = bx + a + ε
Система нормальных уравнений:
an + b∑x = ∑y
a∑x + b∑x2 = ∑yx
Для наших данных система уравнений имеет вид:
10a + 252 b = 40,3
252 a + 8690 b = 938,5
Из первого уравнения выражаем а и подставим во второе уравнение, получаем эмпирические коэффициенты регрессии: b = -0,0329, a = 4,86
Уравнение
регрессии:
Параметр регрессии позволяет сделать вывод о том, что с увеличением количества пропущенных занятий на 4,86 ч, средний балл успеваемости студентов по предметам уменьшится на 0,0329.
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:
Рассчитаем коэффициент детерминации: R2= -0.86392 = 0.7463
Полученный показатель означает, что 75% среднего балла успеваемости студентов объясняется вариацией фактора х – количеством пропущенных занятий.
Далее проведём оценку параметров уравнения регрессии.
- Определим значимость коэффициента корреляции:
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=8 находим tкрит:
tкрит (n-m-1;α/2) = (8;0,025) = 2,06
где m = 1 - количество объясняющих переменных.
Табличное
значение критерия по Фишеру
составляет
.
Т.к.
,
и можно сказать, что уравнение регрессии
является статистически значимым.
- Рассчитаем интервальную оценку для коэффициента корреляции:
, r(-1.0489;-0.6789).
- Проведём анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:
, - необъясненная дисперсия;
- стандартная ошибка оценки;
, - стандартное отклонение случайной величины a.
, - стандартное отклонение случайной величины b.
Рассчитаем доверительные интервалы для параметров регрессии a и b.
,
,
Найдём доверительные интервалы:
и
и
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью p=1-0,05=0,95 параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. являются статистически значимыми и существенно отличны от нуля.
5. Рассчитаем среднюю ошибку аппроксимации:
=
Ошибка аппроксимации в пределах 5%-7% свидетельствует о хорошем подборе уравнения регрессии к исходным данным.