9.4 Граничные соотношения между параметрами помехоустойчивых кодов

Одной из важнейших задач построения помехоустойчивых кодов с заданными характеристиками является установление соотношения между его способностью обнаруживать или исправлять ошибки и избыточностью.

Существуют граничные оценки, связывающие d₀, n и k.

Граница Хэмминга, которая близка к оптимальной для высокоскоростных кодов, определяется соотношениями:

для q-ного кода для двоичного кода

Граница Плоткина, которую целесообразно использовать для низкоскоростных кодов определяется соотношениями:

для q-ного кода для двоичного кода

Границы Хэмминга и Плоткина являются верхними границами для кодового расстояния при заданных n и k, задающими минимальную избыточность, при которой существует помехоустойчивый код, имеющий минимальное кодовое расстояние и гарантийно исправляющий t_u - кратные ошибки.

Граница Варшамова-Гильберта (нижняя граница), определяемая соотношениями:

и

показывает, при каком значении n-k определено существует код, гарантийно исправляющий ошибки кратности t_u.

Лекция 10.

1. Линейные блоковые коды.

2. Порождающая и проверочная матрица.

3. Коды Хемминга.

4. Циклические коды: Хемминга, Боуза - Чоудхури - Хоквингема (БЧХ), Файра, Рида - Соломона.

Порождающие матрицы блочных кодов

Только что в качестве примера были рассмотрены два простейших корректирующих кода - код с простой проверкой на четность, позволяющий обнаруживать однократную ошибку в принятой последовательности, и блочный итеративный код, исправляющий одну ошибку с помощью набора проверок на четность по строкам и столбцам таблицы.

Зададим формальные (порождающие) правила, по которым осуществляется кодирование, то есть преобразование информационной последовательности в кодовое слово.

Простейшим способом описания, или задания, корректирующих кодов является табличный способ, при котором каждой информационной последовательности просто назначается кодовое слово из таблицы кода.

m	U
000	0000
001	0011
010	0101
011	0110
100	1001
101	1010
110	1100
111	1111

Такой способ описания кодов, кстати, применим для любых, а не только линейных кодов. Однако при больших k размер кодовой таблицы оказывается слишком большим, чтобы им пользоваться на практике.

Другим способом задания линейных блочных кодов является использование так называемой системы порождающих уравнений, определяющих правило, по которому символы информационной последовательности преобразуются в кодовые символы. Для того же примера система порождающих уравнений будет выглядеть следующим образом:

u₁ = m₁,

u₂ = m₂,

u₃ = m₃,

u₄ = m₁  m₂  m₃.

Однако наиболее удобным и наглядным способом описания линейных блочных кодов является их задание с использованием порождающей матрицы, являющейся компактной формой представления системы проверочных уравнений.

Линейный блочный (n,k)-код полностью определяется матрицей G размером kn с двоичными матричными элементами. При этом каждое кодовое слово является линейной комбинацией строк матрицы G, а каждая линейная комбинация строк G – кодовым словом.

Обычно порождающие матрицы выглядят так:

Например, для (4,3)-кода с проверкой на четность порождающая матрица будет иметь вид:

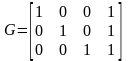
Пусть m = (m₁, m₂,… ,m_k) будет тем блоком-сообщением, который необходимо закодировать с использованием данного кода.

Тогда соответствующим ему кодовым словом U будет

U = m×G

С учетом структуры матрицы G символы кодового слова U будут такими:

для i = 1, 2,... , k:

u_i = m_i ;

для i = k+1,... , n:

u_i = m₁× P_1,i-k  m₂× P_2,i-k  m₃× P_3,i-k … m_k× P_k,i-k .

Иными словами, k крайних левых символов кодового слова совпадает с символами кодируемой информационной последовательности, а остальные (n - к) символов являются линейными комбинациями символов информационной последовательности.

Например, если входная последовательность кодера m = (1 0 1), то с применением порождающей матрицы код будет построен так:

,

Определенный таким образом код называется линейным блочным систематическим (n,k)-кодом с обобщенными проверками на четность, а задающая его матрица G называется порождающей матрицей кода.