3.5. Примерная схема построения графика функции

С учетом всего вышеописанного для исследования функции и дальнейшего построения графика следует придерживаться следующей схеме:

1. Область существования функции.

2. Симметрия графика функции (четность, нечетность).

3. Точки пересечения графика функции с осями координат.

4. Использование первой производной: интервалы возрастания и убывания, экстремумы функции.

5. Использование второй производной: участки выпуклости и вогнутости графика, точки перегиба.

6. Составление сводной таблицы результатов исследования.

7. Построение графика.

Пример. Исследовать функцию и построить ее график

Решение.

1. Найдем область определения функции. Дробь определена, если знаменатель отличен от нуля, т. е.

; .

И так, .

2. Исследуем функцию на четность. Так как точка не входит в область определения функции, а точка принадлежит области определения функции, т. е. область определения рассматриваемой функции не симметрична относительно начала координат, то функция не является чётной и не является нечётной.

3. Найдём точки пересечения графика функции с осями координат − с осью :

; ; .

и осью : , .

График функции пересекается с координатными осями в начале координат − точке .

4. Определим экстремумы и интервалы монотонности функции. Для этого найдём первую производную и решим уравнение ;

;

;

;

.

Функция возрастает при и убывает при .

Поскольку при переходе через точку первая производная меняет знак с «-» на «+», то это точка минимума:

.,

а при переходе через точку первая производная меняет знак с «+» на «-», то это точка максимума:

Итак, − точка локального минимума, – точка локального максимума.

5. Найдем интервалы выпуклости и вогнутости графика функции и точки перегиба. Для этого найдём вторую производную и решим уравнение :

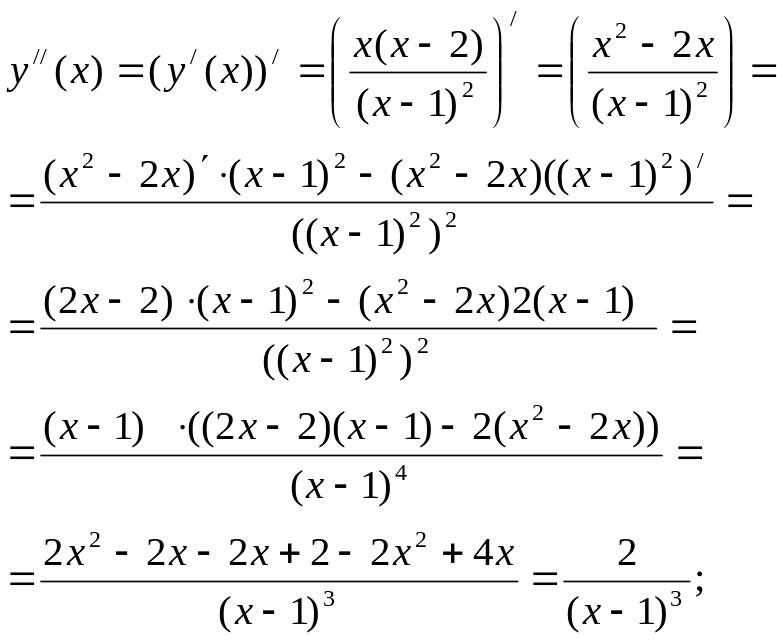
Левая часть данного уравнения в нуль никогда не обращается точек перегиба нет.

Исследуем знак на промежутках :

;

.

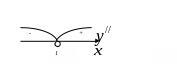
График функции выпуклый вверх при ; вогнутый − при .

6. Составим сводную таблицу.

	+	0	–	Не сущ.	–	0	+
	–	-2	–	Не сущ.	+	2	+
		0		Не сущ.		4
		max				min

7. Постоим график.

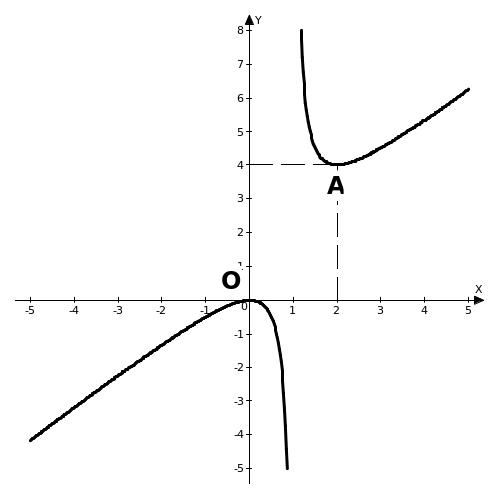
§ 4. Неопределенный интеграл

Ранее мы рассматривали способы нахождения производных функции, а также их применение к исследованию функций, что составляет основную задачу раздела высшей математики, называемого дифференциальным исчислением. Далее перейдем к рассмотрению основ интегрального исчисления, которое решает обратную задачу, а именно задачу нахождения функции по ее производной или дифференциалу.