3.3.Определение промежутков возрастания и убывания , а также экстремумов функции с помощью производной

Исследование функции на наличие участков возрастания и убывания функции, а также существование экстремумов с помощью производной осуществляется по следующей схеме:

1. находят область определения функции;

2. находят производную функции;

3. приравнивают производную функции к нулю и решают полученное уравнение . Корни данного уравнения (если они имеются) являются стационарными точками функции.

4. находят критические точки и точки, в которых производная не существует и отмечают их на числовой оси в порядке возрастания;

5. определяют знаки производной на интервалах, на которые делят числовую ось критические точки и отмечают полученные результаты над соответствующими интервалами;

6. с учетом знака производной находят интервалы возрастания (на них производная положительная) и убывания (на них производная отрицательная);

7. находят точки экстремумов функции (т. е. точки, при переходе через которые знак производной меняется на противоположный).

Пример. Найти промежутки возрастания и убывания функции, а также экстремумы функции

Решение.

1. Найдем область определения функции. Дробь определена, если знаменатель отличен от нуля, т. е.

; ; ; .

И так, .

2. Найдем производную функции

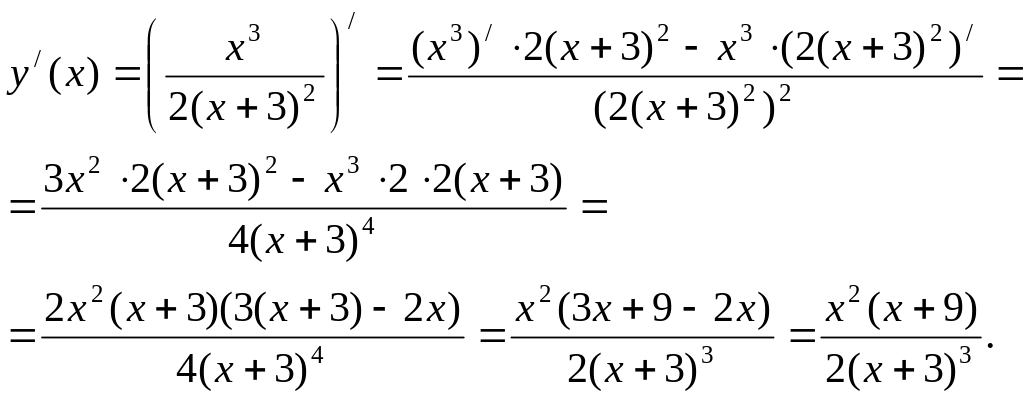
3. Приравняем производную к нулю и решим уравнение ;

4. Найденные критические точки и точки, в которых производная не существует, отметим на числовой оси в порядке возрастания

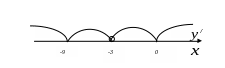
5. Определим знаки производной на интервалах, на которые делят числовую ось критические точки и отметим полученные результаты над соответствующими интервалами;

;

;

;

.

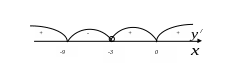
6. С учетом знака производной находим интервалы возрастания (на них производная положительная) и убывания (на них производная отрицательная). Функция возрастает при и убывает при .

7. Находим точки экстремумов функции (т. е. точки, при переходе через которые знак производной меняется на противоположный).

Поскольку при переходе через точку первая производная меняет знак с «+» на «-», то это точка максимума:

.

Итак, − точка локального максимума.

3.4. Выпуклость и вогнутость графика функции. Точки перегиба

Определение. График функции называют выпуклым в точке с абсциссой , если в некоторой -окрестности точки график функции лежит под касательной к нему, проведенной в этой точке (рис. 6).

Определение. График функции называют вогнутым в точке с абсциссой , если в некоторой -окрестности точки график функции лежит над касательной к нему, проведенной в этой точке (рис. 7).

Определение. Точки, в которых график функции переходит с одной стороны своей касательной на другую, то есть пересекает свою касательную, называют точками перегиба (рис. 8).

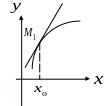
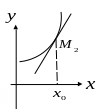
Рис. 6. Рис. 7.

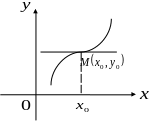
Рис. 8.

Теорема. Достаточный признак выпуклости или вогнутости функции в некоторой точке с абсциссой ( при условии, что при функция имеет непрерывную вторую производную) состоит в следующем: если , то график функции в этой точке выпуклый; если , то график функции в этой точке вогнутый.

Из достаточного признака выпуклости и вогнутости графика функции получаем необходимый признак наличия точек перегиба: в точке перегиба вторая производная функции либо равна нулю, либо не существует.

Теорема. Достаточный признак наличия или отсутствия точки перегиба: если слева и справа от критической точки имеются такие промежутки и (где - некоторое положительное число), в каждом из которых сохраняет постоянный знак, то точка будет точкой перегиба, если знаки в этих промежутках разные, и не будет ею, если знаки в этих промежутках одинаковые.