§ 3.Применение производных при исследовании функций
Возможность применения производных при исследовании функций основана на связи, существующей между производными функций и некоторыми особенностями графиков этих функций.
3.1.Связь производной функции с наличием промежутков ее возрастания и убывания
Как мы уже говорили, функция называется возрастающей на интервале , если для любых двух значений и , принадлежащих этому интервалу и удовлетворяющих неравенству , выполняется неравенство , и убывающей, если при этих же условиях выполняется неравенство .
Теорема 1.
Если функция дифференцируема и возрастает на интервале , то производная этой функции не отрицательна
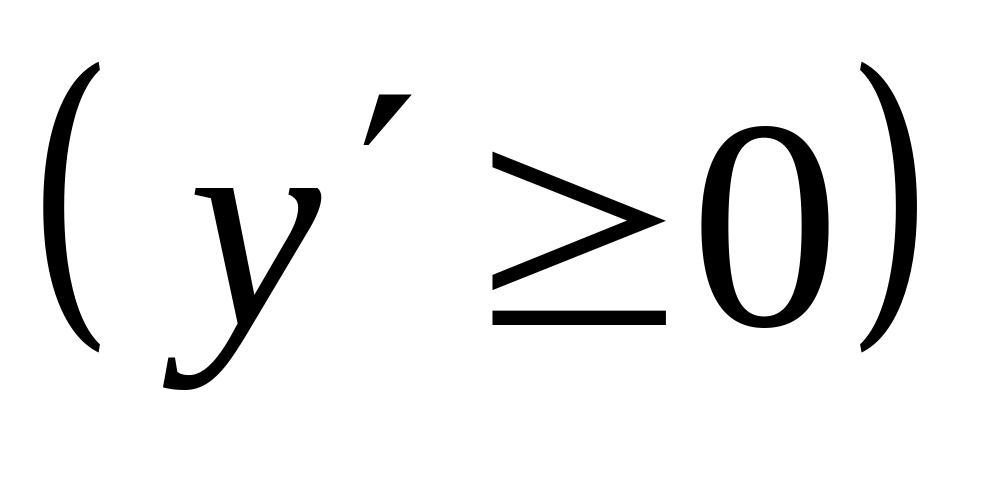во
всех точках данного интервала.Если функция дифференцируема и убывает на интервале , то производная этой функции не положительна
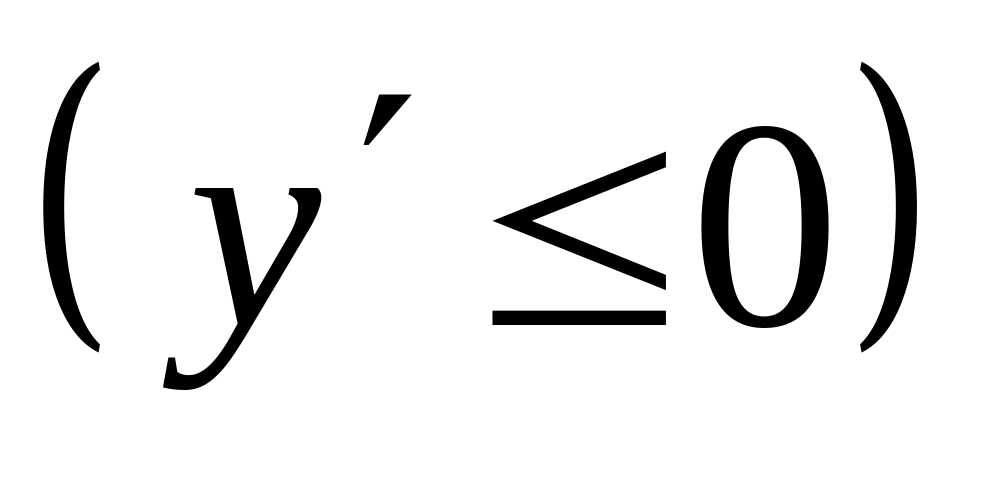во
всех точках данного интервала.
Эту теорему называют теоремой о необходимых признаках возрастания и убывания функции, поскольку в ней указывается, какой должна быть производная дифференцируемой функции на интервале в случаях соответственно возрастания и убывания функции.
Необходимо помнить, что неотрицательность производной является лишь необходимым, но не достаточным условием для утверждения о возрастании функции, точно так же, как неположительность производной не является достаточным условием для утверждения о ее убывании.
Теорема 2.
Если производная функции положительна
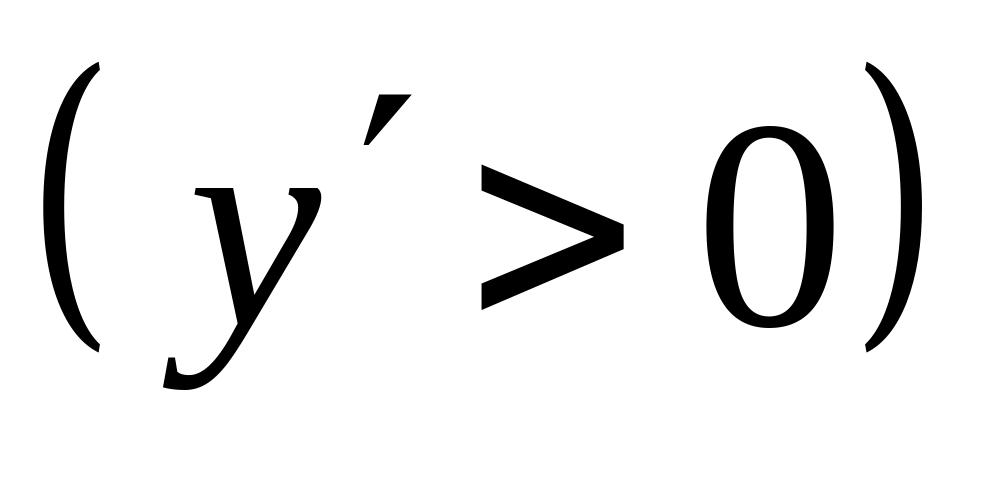на интервале
,то
функция возрастает на этом интервале.Если производная функции отрицательна
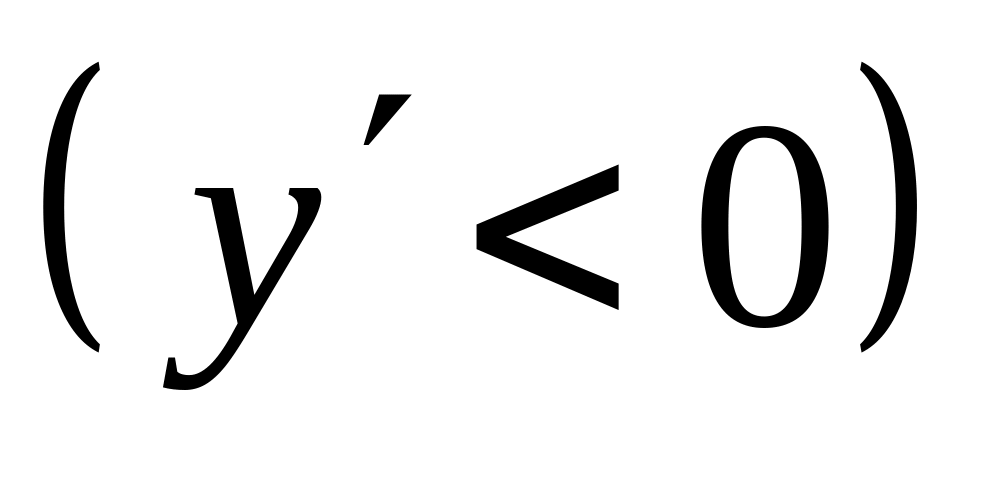на интервале
,то
функция убывает на этом интервале.
Эту теорему называют теоремой о достаточных признаках возрастания и убывания функции, поскольку в ней указывается, при каком знаке производной на интервале дифференцируемая функция возрастает и при каком – убывает.
3.2.Связь производной с наличием экстремумов функции
Определение.
Точка
(рис.4) называется точкой
максимума функции
,
если существует такая окрестность этой
точки, что для всех значений
,
принадлежащих этой окрестности,
выполняется неравенство:
.
Определение.
Точка
(рис.5) называется точкой
минимума функции
,
если существует такая окрестность этой
точки , что для всех значений
,
принадлежащих этой окрестности, кроме
выполняется неравенство:
.
Определение. Точками экстремумов функции называют точки, в которых функция принимает минимальные или максимальные значения.
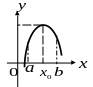
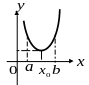
Рис.4 Рис.5
Если точек максимумов или минимумов несколько, то такие максимумы или минимумы называют локальными.
Существует тесная связь между наличием экстремумов у дифференцируемых функций и поведением их производных в соответствующих точках и их окрестностях.
Теорема. Производная дифференцируемой функции в точке экстремума равна нулю.
Эту теорему называют теоремой о необходимом условии существования экстремума дифференцируемой функции в точке, поскольку в ней указывается, что если дифференцируемая функция имеет в некоторой точке экстремум, то в этой точке производная функции обязательно равна нулю.
Из рассмотренной теоремы вытекает, что дифференцируемая функция может иметь экстремумы лишь в тех точках, где ее производная равна нулю, т. е. в так называемых стационарных точках функции, являющихся корнями уравнения:
.
Теорема.
Если производная функции
в некоторой точке
обращается в нуль и при переходе через
эту точку изменяет свой знак на
противоположный, то данная точка является
точкой экстремума функции, причем:
этот экстремум является максимумом, если при переходе через точку слева направо знак производной изменяется с положительного на отрицательный;
этот экстремум является минимумом, если при переходе через точку слева направо знак производной изменяется с отрицательного на положительный.
Эту теорему называют теоремой о достаточных условиях существования экстремума дифференцируемой функции в точке, поскольку в ней указаны те условия, которым должна удовлетворять производная, чтобы функция в рассматриваемой точке имела экстремум определенного типа.
Справедливо следующее утверждение: точками экстремумов являются лишь те из критических точек функции, при переходе через которые знак производной изменяется на противоположный; при этом изменение знака с плюса на минус свидетельствует о наличии точки максимума, а с минуса на плюс – точки минимума.