2.6. Производная сложной функции

Теорема. Если функция определена и дифференцируема на интервале , причем областью ее значений является интервал , а функция определена и дифференцируема на интервале , то производная сложной функции существует и равна произведению производной внешней функции по ее аргументу на производную внутренней функции по ее аргументу :

,

Причем в этой формуле при обозначении производных под штрихом в виде индексов указаны переменные, по которым ведется дифференцирование.

Пример. Найти производную сложной функции .

Т. к. данная функция является сложной, то введем в рассмотрение внутреннюю функцию и внешнюю функцию . С учетом этих обозначений исходная функция может быть представлена в виде и для нахождения ее производной применяем формулу :

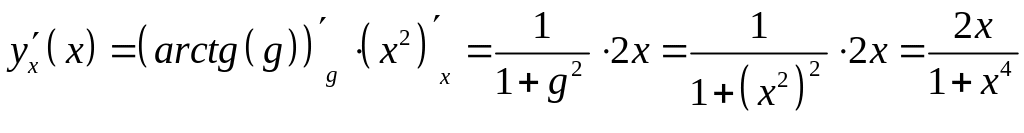
2.7. Метод логарифмического дифференцирования

Во многих случаях оказывается целесообразным прежде чем дифференцировать заданную функцию, взять ее логарифм, определить затем производную от этого логарифма, а затем найти производную заданной функции. Такой прием называется методом логарифмического дифференцирования. Этот метод позволяет легко найти производную от сложной функции вида , где и есть функции зависящие от .

Пусть дана функция .

1. 4.

2. 5.

3. 6.

Пример. Найти производную функции .

Применим метод логарифмического дифференцирования.

1.

2.

3.

4.

5. 6.

2.8. Дифференцирование логарифмической функции

Дифференцирование логарифмической функции рассмотрим на примере.

Пусть дана функция . Выполним некоторые преобразования, пользуясь общими правилами логарифмирования и свойствами логарифмов:

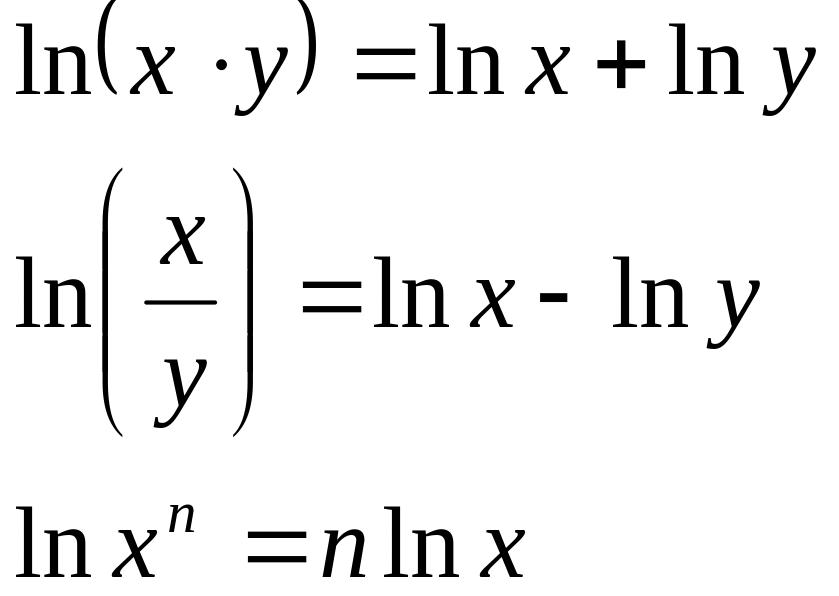
Получим .

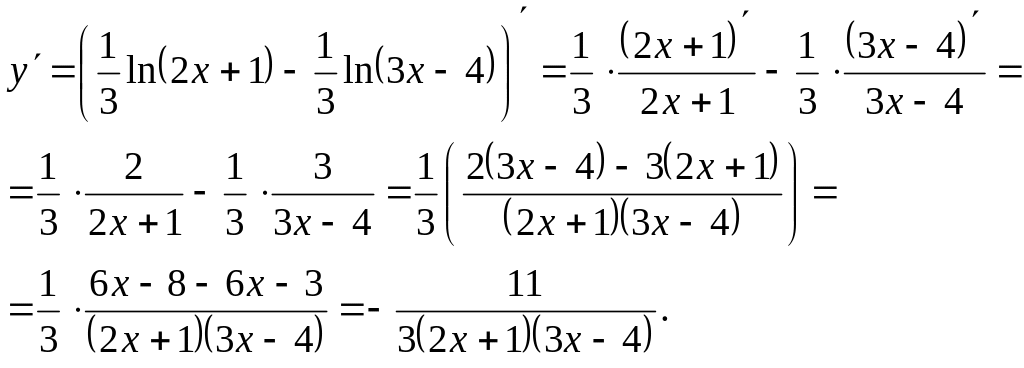
2.9. Производные высших порядков

Производную называют еще первой производной, или производной первого порядка, функции в отличие от так называемых производных высших порядков.

Производная функции в общем случае представляет собой некоторую новую функцию, которая в свою очередь тоже может быть дифференцируемой. Следовательно, можно найти производную и этой функции, представляющую собой производную от производной исходной функции и называемую второй производной, или производной второго порядка, исходной функции. Производную второго порядка принято обозначать .

Производную от производной второго порядка, если она существует, называют третьей производной функции , или производной третьего порядка, и обозначают или и т. д.

Определение. Производные порядков выше первого называются производными высших порядков.

При этом производная -го порядка определяется как производная от производной предыдущего порядка, т. е.

.

Пример. Найти вторую производную функции .

Найдем сначала первую производную .

Найдем вторую производную