2.2. Физический смысл производной

Мгновенная скорость прямолинейного движения материальной точки равна производной зависимости ее координаты от времени

.

Применительно к процессам размножения бактерий и протекания химической реакции производная функции, характеризующей соответствующий процесс, представляет собой скорость течения этого процесса во времени.

В общем случае производная функции представляет собой скорость изменения этой функции при изменении ее аргумента. В этом и состоит физический смысл (физическая интерпретация) производной функции.

2.3. Геометрический смысл производной

Производная функции в точке имеет достаточно простую геометрическую интерпретацию.

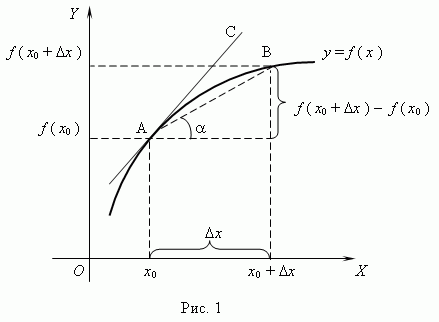
Пусть дана кривая . Возьмем на ней точку и дадим аргументу приращение . Тогда получим новый аргумент и новое значение функции , т. е. мы получили новую точку на кривой и обозначим её через . Проведем секущую и обозначим угол наклона секущей к оси через . Рассмотрим прямоугольный треугольник :

.

При точка перемещается вдоль кривой, приближаясь к точке . Секущая поворачивается вокруг точки и величина угла изменяется. При приближении секущей к касательной угол приближается к углу .

.

Так как в математике величину угла наклона касательной, проведенной к графику функции называют угловым коэффициентом касательной, то из полученной формулы следует, что угловой коэффициент касательной, проведенной к графику дифференцируемой функции в некоторой точке, численно равен производной функции в данной точке.

Это и есть геометрический смысл производной.

Уравнение касательной: .

Уравнение нормали: .

2.4. Производные основных элементарных функций

1. 1.

2. 2.

3. 3.

4. 4.

5. 5.

6. 6.

7. 7.

8. 8.

9. 9.

10. 10.

11. 11.

12. 12.

13. 13.

2.5. Основные правила дифференцирования функций

Правило 1. Производная константы (постоянной величины) равна нулю .

Правило 2. Производная аргумента равна единице .

Правило 3. Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций .

Пример.

Правило 4. Производная произведения двух дифференцируемых функций равна сумме произведений производной первой функции на вторую и первой функции на производную второй .

Пример.

Следствие из правила 4. Производная произведения постоянного множителя на дифференцируемую функцию равна произведению этого множителя на производную данной функции .

Пример.

Правило 5. Производная частного двух дифференцируемых функций ( при условии, что знаменатель не обращается в нуль) равна дроби, числитель которой представляет собой разность между произведением производной первой функции на вторую и произведением первой функции на производную второй, а знаменатель равен квадрату второй функции .

Пример.

.