1.4. Преобразования графиков функций

Иногда бывает важным построить график функции отталкиваясь от графика той или иной элементарной функции с помощью определенных правил преобразования графиков функции или используя правила построения графиков сложных функции.

Приведем некоторые простейшие методы построения графиков функции.

График функции может быть получен из графика функции с помощью простых геометрических преобразований. Приведем их в таблице:

y=f(x)+A	Параллельный перенос его вдоль оси OY на А единиц вверх, если А>0 и на |A| единиц вниз, если A<0.
y=f(x-a)	Параллельный перенос его вдоль оси ОY на a единиц вправо, если а>0, и на -а единиц влево, если a<0.
y=kf(x), k>0	Растяжение вдоль оси ОХ в k раз, если k>1, и сжатие в 1/k раз, если 0<k<1.
y=f(kx), k>0	Сжатие вдоль оси ОХ относительно оси OY в k раз, если k>1 и растяжение в 1/k раз, если 0<k<1.
y=-f(x)	Симметричное отображение графика относительно оси ОХ.
y=|f(x)|	Часть графика функции y=f(x), расположенная ниже оси ОХ, симметрично отражается относительно этой оси, остальная часть графика остается без изменения.
y=f(-x)	Симметричное отображение графика относительно оси ОY.
y=f(|x|)	Часть графика функции y=f(x), расположенная в области x0, остается без изменения, а его часть для области x0 заменяется симметричным отображением относительно оси OY.

§2. Производная функции

Понятие производной – одно из основных понятий математического анализа. Его значимость заключается в том, что производная функции характеризует скорость изменения этой функции при изменении ее аргумента.

2.1. Производная функции

y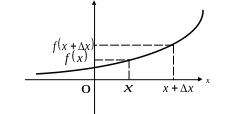

Рассмотрим некоторую непрерывную функцию (т. е. функцию, графически представляемую непрерывной линией), характеризующую зависимость от , причем ее график имеет вид, представленный на рис. 1.

Рис.2.

Когда аргумент функции получает приращение , функция получает приращение . Значения и должны принадлежать области определения функции.

При уменьшении приращения аргумента приращение функции также уменьшается и их отношение в общем случае претерпевает некоторое изменение.

Определение. Производной функции в точке называется предел приращения функции к приращению аргумента , когда стремиться к нулю , при условии что этот предел существует.

.

.

Процесс нахождения производной называется дифференцированием.

Определение. Функция, для которой в точке существует конечная производная, называется дифференцируемой в данной точке.

Если функция имеет конечные производные во всех точках некоторого промежутка, то она называется дифференцируемой на данном промежутке.

Существуют следующие обозначения производной: