§ 3. Математическая статистика.

Задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов.

Пусть требуется изучить совокупность однородных объектов относительно некоторого количественного или качественного признака, характеризующего эти объекты.

Выборочной совокупностью или просто выборкой называется совокупность случайно отобранных объектов.

Генеральной совокупностью называется совокупность объектов, из которых производиться выборка.

Наблюдаемые значения называются вариантами, а последовательность вариант, записанная в возрастающем порядке, называется вариационным рядом.

Число наблюдений называется частотами (обозначаются ), а их отношение к объему выборки (обозначается ) называется относительными частотами.

Статистическим распределением выборки называется перечень вариант и соответственно их частот (относительных частот).

Статистическое распределение можно задать так же в виде последовательности интервалов и соответствующих им частот.

Пример 1. Составит статистическое распределение и вариационный ряд следующей выборки: 2,1,1,1,3,4,2.

	1	2	3	4
	3	2	1	1

1,1,1,1,1,3,4 – вариационный ряд.

Для оценки плотности распределения используют полигон и гистограмму частот.

Полигоном частот называют ломаную, отрезки которой соединяют точки .

Полигоном относительных частот называют ломаную, отрезки которой соединяют точки .

Если признак непрерывен, то используют гистограмму частот.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основанием которых служат частичные интервалы длиной , а высоты равны отношению .

Статистическое распределение обладает следующими числовыми характеристиками:

1. выборочная средняя ;

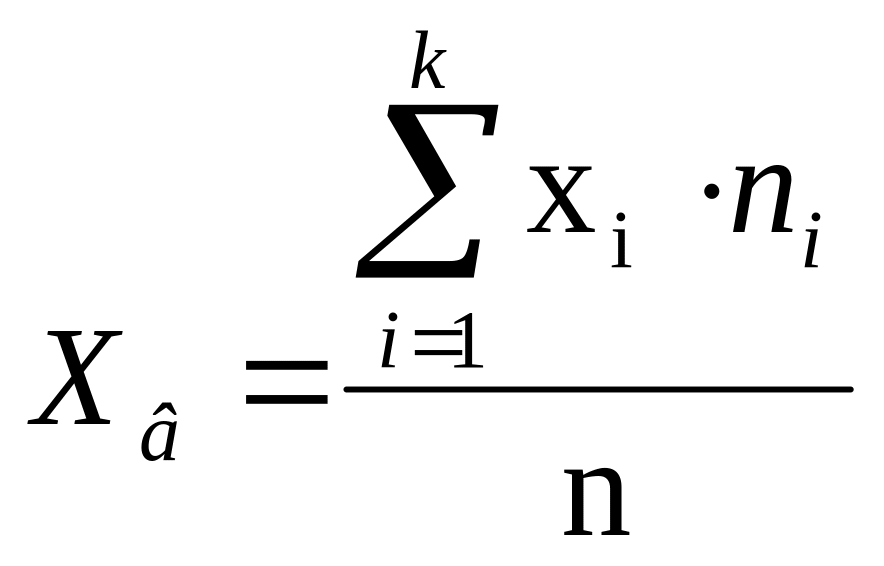2. выборочная дисперсия ;

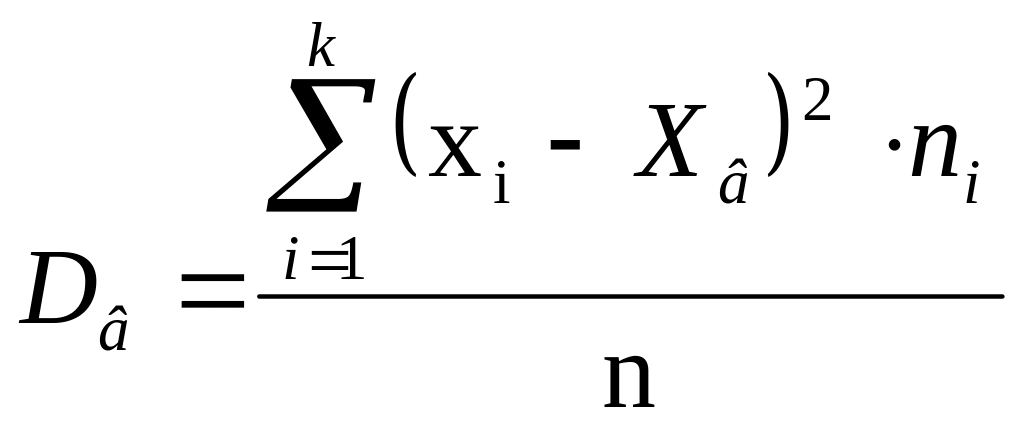3. исправленная дисперсия ;

4. среднеквадратическое отклонение .

Доверительным называется интервал, который с заданной надежностью покрывает оцениваемый параметр.

Для оценки математического ожидания случайной величины , распределенной по нормальному закону, при известном среднеквадратическом отклонении служит доверительный интервал

где - точность оценки, - объем выборки, - выборочное среднее, - аргумент функции Лапласа (табличное значение).

Пример 2. У семи человек продолжительность инкубационного периода вирусным гепатитом составила: 17,1; 16,2; 18,3; 16,6; 15,3; 18,6; 16,4; 16,5; 17,5; 16,9 дней. Требуется: 1) определить выборочную среднюю , выборочную D_в и исправленную S² дисперсии; 2) полагая, что распределение признака Y описывается нормальным законом распределения, найдите доверительный интервал для средней продолжительности инкубационного периода а у обследуемых людей на уровне заданной надежности  = 0,999.

Решение.

1. Определим выборочную среднюю , выборочную D_в и исправленную S² дисперсии. Вспомогательные расчеты проведем в таблице.

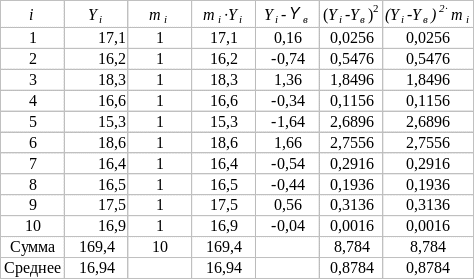
Выборочная средняя .

Выборочная дисперсия D_в .

Исправленная дисперсия s^{2 .}

2. Полагая, что распределение признака Y описывается нормальным законом распределения, найдём доверительный интервал для средней продолжительности инкубационного периода а у обследуемых людей на уровне заданной надежности  = 0,999. Доверительный интервал найдём по формуле:

, где . по таблице (см. приложение 3 в [ 8 ]) по заданным n=10  = 0,999 находим t_=4,78.

Итак, и доверительный интервал

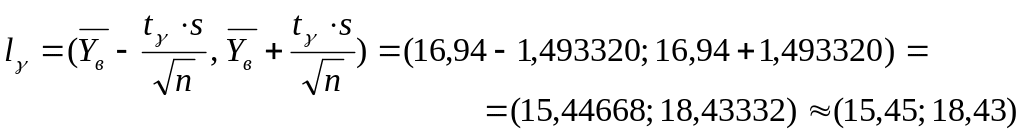
Ответ: Выборочная средняя ; выборочная дисперсия D_в ; исправленная дисперсия s^{2 .}

С надёжностью 0,999 средняя продолжительность инкубационного периода у обследуемых людей а заключена в доверительном интервале 15,45 < а < 18,43.