1.5. Повторные независимые испытания
При практическом применении теории вероятностей часто приходиться встречаться с задачами, в которых один и тот же опыт повторяется неоднократно. В результате каждого опыта может появиться или нет некоторое событие , причем нас интересует не результат каждого отдельного опыта, а общее число появления события в результате серии опытов.
Определение. Повторными независимыми испытаниями называют испытания, удовлетворяющие следующим условиям:
1) количество испытаний конечно;
2) вероятность
осуществления случайного события
в каждом из испытаний постоянна:
.
Определение. Опыты называются независимыми, если вероятность того или иного исхода каждого из опытов не зависит от того, какие исходы имели другие опыты.
Примером повторных независимых испытаний могут служить многочисленные подбрасывания монеты.
Пусть производится
независимых
испытаний. Вероятность появления события
для каждого испытания одинакова и равна
.
Какова вероятность того, что событие
появится ровно
раз из
?
– {событие появится ровно раз из }
Эта формула называется формулой Бернулли.
Пример. Монета бросается 5 раз. Найти вероятность того, что ровно 3 раза выпадет герб.
Решение.
– {ровно 3 раза выпадет герб}
–
вероятность выпадения
герба при одном бросании
–
вероятность не
выпадения герба при одном бросании
,
Ответ: вероятность
того, что ровно 3 раза выпадет герб равна,
.
При больших значениях
вычисления вероятностей
по формуле Бернулли становиться
затруднительно. Однако в ряде случаев
удается заменить её приближенными
формулами:
1. если велико и мало, то применяют формулу Пуассона
2. если велико и близко к единице, то применяют локальную формулу Муавра – Лапласа
,
3. если велико и близко к единице, то применяют интегральную формулу Муавра – Лапласа
Если
,
то
.
Пример.
§ 2. Случайные величины
Определение. Величина, принимающая те или иные числовые значения в зависимости от различных случайных обстоятельств, называется случайной величиной.
Примерами случайных величин являются: количество груш на дереве, количество посетителей стоматологической клиники в течение дня, продолжительность человеческой жизни и т. д.
Случайные величины бывают:
1. дискретные (ДСВ);
2. непрерывные (НСВ).
Определение:
Случайная величина
называется дискретной, если она принимает
конечное или счетное число своих
значений.
Определение: Случайная величина называется непрерывной, если она принимает несчетное число своих значений.
Обозначают случайные
величины заглавными буквами латинского
алфавита
и их возможные значения соответственно
Вероятности случайных величин обозначают буквами с соответствующими индексами:
.
Определение. Законом распределения (рядом распределения) ДСВ называется перечень всех значений случайной величины и соответствующих им вероятностей.
Ряд распределения можно задать:
1. таблично
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. графически
Определение. Многоугольником распределения случайной величины называется ломаная, отрезки которой соединены точками.
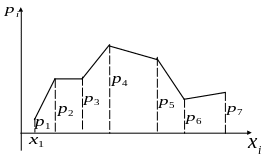
Вероятность многих дискретных величин вычисляются с помощью формул сложения и умножения вероятностей или с помощью формулы Бернулли.
В зависимости от того, как определяются вероятности ДСВ, можно выделить основные законы распределения:
1. равномерное распределение;
2. геометрическое распределение;
3. гипергеометрическое распределение;
4. биномиальное распределение.
Пример. Составит закон распределения ДСВ – числа рождения девочки у трех рожениц.
Решение.
|
0 |
1 |
2 |
3 |
|
0,125 |
0,375 |
0,375 |
0,125 |
– вероятность рождения девочки
– вероятность рождения мальчика
