1.3. Теоремы сложения и умножения вероятностей .

Теорема 1. Вероятность суммы конечного числа несовместных событий равна сумме их вероятностей:

Пример. Вероятность того, что в магазине будет продана пара мужской обуви 44-го размера, равна 0,12; 45-го – 0,04; 46-го и большего – 0,01. Найти вероятность того, что будет продана пара мужской обуви не меньше 44-го размера.

Решение. Искомое событие произойдет, если будет продана пара обуви 44-го размера (событие ) или 45-го (событие ), или не меньше 46-го (событие С), т. е. событие есть сумма событий . События , и несовместны. Поэтому согласно теореме о сумме вероятностей получаем

Теорема 2. Вероятность суммы двух совместных событий вычисляется по формуле

Теорема 3. Вероятность наступления хотя бы одного из нескольких независимых событий вычисляется по формуле

,

Если все вероятности одинаковые, т. е. , то формула перепишется в виде

Пример . Найти вероятность того, что хотя бы один студент из 20 заболеет гриппом, если вероятность заболеть 0,2.

Решение.

– «хотя бы один студент из 20-ти заболеет гриппом»

Ответ: вероятность того, что хотя бы один студент из 20 заболеет гриппом, равна 0,988471.

Теорема 4. Вероятность произведения нескольких независимых событий вычисляется по формуле

Пример. Три стрелка одновременно стреляют в мишень. Вероятности попадания равны 0,9,08 и 0,7 соответственно. Найти вероятность того, что все стрелки попадут в мишень.

Решение.

– «все три стрелка попадут в мишень»

– « i-й стрелок попадет в мишень»,

Ответ: вероятность того, что все три стрелка попадут в мишень равна 0,504.

Теорема 5. Вероятность одновременного наступления нескольких зависимых событий вычисляется по формуле

,

где – условные вероятности.

Пример. Найти вероятность того, что выпадут три туза из колоды 36 карт.

Решение.

– «выпадут три туза»

Ответ: вероятность того, что выпадут три туза, равна 0,00056.

1.4. Формула полной вероятности и формула Байеса

Теорема 1. Если событие может наступить при условии наступления одного из событий , то вероятность этого события находят по формуле полной вероятности

Теорема 2. Событие может наступить при условии наступления одного из событий . Известно, что событие наступило. Тогда вероятность одного из событий находят по формуле Байеса.

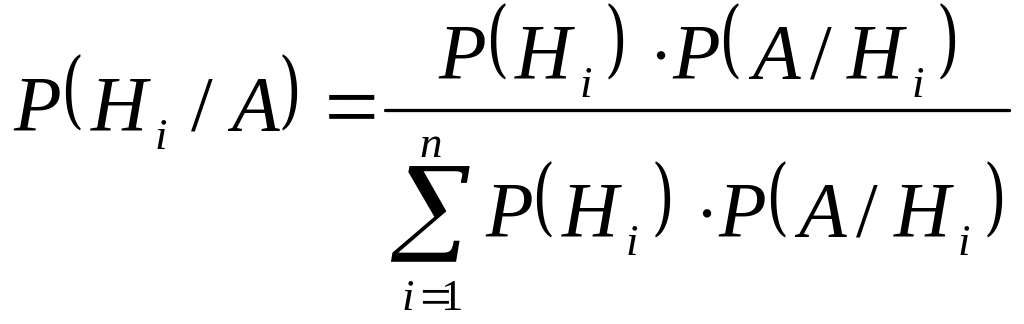
Определение. Совокупность случайных событий называется полной группой событий для данного испытания, если в результате испытания обязательно происходит только одно из событий этой совокупности.

Следствие.

Пример. В магазин поступила новая продукция с трех предприятий. Процентный состав этой продукции следующий: 20% - продукция первого предприятия, 30% - продукция второго предприятия, 50% - продукция третьего предприятия; далее, 10% продукции первого предприятия высшего сорта, на втором предприятии - 5% и на третьем - 20% продукции высшего сорта. Найти вероятность того, что случайно купленная новая продукция окажется высшего сорта.

Решение.

А ={ будет куплена продукция высшего сорта }

= { куплена продукция, принадлежащая предприятию},

Можно применить формулу полной вероятности, причем в наших обозначениях:

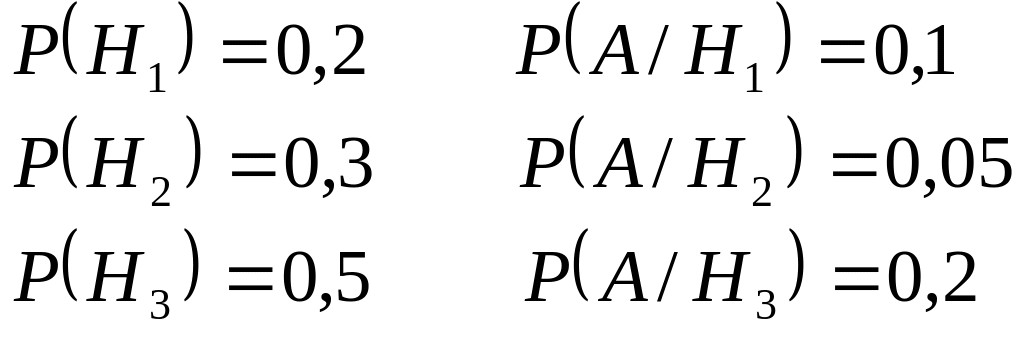
Подставляя эти значения в формулу полной вероятности, получим искомую вероятность:

Ответ: вероятность того, что случайно купленная новая продукция окажется высшего сорта, равна 0,135.

Пример. На трех станках-автоматах обрабатываются однотипные детали, поступающие после обработки на общий конвейер. Первый станок дает 2% брака, второй – 7%, третий – 10%. Производительность первого станка в 3 раза больше производительности второго, а третьего – в 2 раза меньше, чем второго.

а) Каков процент брака на конвейере?

б) Каковы доли деталей каждого станка среди бракованных деталей на конвейере?

Решение.

Возьмем с конвейера наудачу одну деталь и рассмотрим событие А – деталь бракованная. Оно связано с гипотезами относительно того, где была обработана эта деталь: – взятая наудачу деталь обработана на -ом станке, .

Условные вероятности (в условии задачи они даны в форме процентов):

Зависимости между производительностями станков означают следующее:

.

А так как гипотезы образуют полную группу, то

.

Решив полученную систему уравнений, найдем:

.

а) Полная вероятность того, что взятая наудачу с конвейера деталь – бракованная:

.

Другими словами, в массе деталей, сходящих с конвейера, брак составляет 4%.

б) Пусть известно, что взятая наудачу деталь – бракованная. Пользуясь формулой Байеса, найдем условные вероятности гипотез:

,

,

.

Таким образом, в общей массе бракованных деталей на конвейере доля первого станка составляет 33%, второго – 39%, третьего – 28%.