2. Биомасса популяции.

Рассмотрим популяцию, в которой масса особи заметно меняется в течение жизни, и подсчитаем общую биомассу популяции.

Пусть означает возраст в тех или иных единицах времени, а — число особей популяции, возраст которых равен . Пусть, наконец, — средняя масса особи возраста , а — био­масса всех особей в возрасте от до .

Заметив, что произведение равно биомассе всех осо­бей возраста , рассмотрим разность

,

где . Очевидно, что эта разность, равная биомассе всех осо­бей в возрасте от до , удовлетворяет неравенствам:

,

где — наименьшее, а - — наибольшее значения функции на отрезке . Учитывая, что , из неравенств

,

имеем:

.

Из непрерывности функции (ее непрерывность следует из непрерывности и ) следует, что

Поэтому будем иметь:

или

.

Следовательно, биомасса является перво­образной для . Отсюда:

где — максимальный возраст особи в данной популяции. Так как , очевидно, равно нулю, то окончательно получаем:

.

3. Средняя длина пролета.

В некоторых исследованиях необхо­димо знать среднюю длину пробега, или среднюю длину пути при прохождении животным некоторого фиксированного участка. При­ведем соответствующий расчет для птиц. Пусть участком будет круг радиуса . Будем считать, что не слишком велико, так что большинство птиц изучаемого вида пересекает этот круг по прямой.

Птица может под любым углом в любой точке пересечь окруж­ность. В зависимости от этого длина ее пролета над кругом может быть равной любой величине от до . Нас интересует средняя длина пролета. Обозначим ее через .

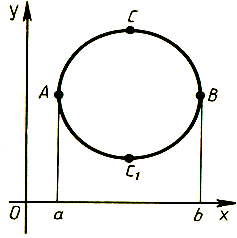
Так как круг симметричен относительно любого своего диамет­ра, нам достаточно ограничиться лишь теми птицами, которые ле­тят в каком-нибудь одном направлении, параллельном оси . Тогда средняя длина пролета — это среднее расстоя­ние между дугами и . Иными словами, это среднее зна­чение функции , где — уравнение верхней дуги, а у — уравнение нижней дуги, т. е.

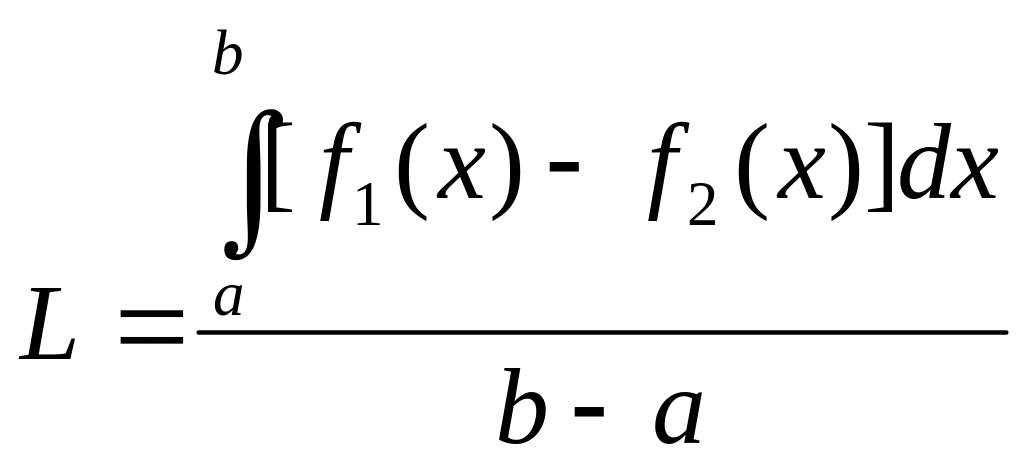или .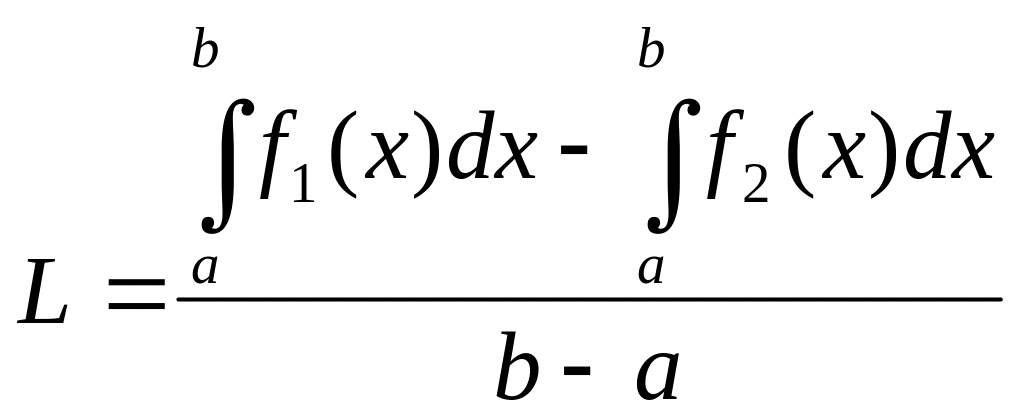

Так как равен площади криволинейной трапеции , а равен площади криволинейной трапеции , то их разность равна площади круга, т. е. . Разность равна, очевидно, . Подставив это в , получим:

.

Приведенные примеры далеко не исчерпывают возможных приложений определенного интеграла в биологии.

§ 6. Дифференциальные уравнения

Математическое описание различных процессов и явлений – физических, химических, биологических и т. д. – часто содержит уравнения, в которых присутствуют не только изучаемые величины, но и производные различных порядков от этих величин.

6.1. Основные понятия и определения дифференциальных уравнений

Определение. Дифференциальным уравнением называется уравнение, связывающее независимую переменную, неизвестную функцию и её производные различных порядков.

Дифференциальное уравнение относительно одной независимой переменной называется обыкновенным.

Порядком дифференциального уравнения называется порядок старшей производной, входящей в него.

Например: – ДУ 1-го порядка

– ДУ 2-го порядка

Общий вид обыкновенного дифференциального уравнения определяется следующим выражением:

(1)

Определение. Решением дифференциального уравнения называется такая функция , которая будучи подставленной в уравнение вместе со своими производными, обращает его в тождество (верное равенство).

График решения дифференциального уравнения называется интегральной кривой.

Определение. Общим решением дифференциального уравнения (1) называется функция вида

(2)

Если в (2) постоянным придать конкретные числовые значения, то полученная функция называется частным решением дифференциального уравнения.