- •Введение.
- •Глава 1. Математический анализ
- •§1. Функции
- •1.1. Функциональная зависимость
- •1.2. Способы задания функций
- •1.3. Графики элементарных функцй
- •1.4. Преобразования графиков функций
- •§2. Производная функции
- •2.1. Производная функции
- •2.2. Физический смысл производной
- •2.3. Геометрический смысл производной
- •2.4. Производные основных элементарных функций
- •2.5. Основные правила дифференцирования функций
- •2.6. Производная сложной функции
- •2.7. Метод логарифмического дифференцирования
- •2.8. Дифференцирование логарифмической функции
- •2.9. Производные высших порядков
- •§ 3.Применение производных при исследовании функций
- •3.1.Связь производной функции с наличием промежутков ее возрастания и убывания
- •3.2.Связь производной с наличием экстремумов функции
- •3.3.Определение промежутков возрастания и убывания , а также экстремумов функции с помощью производной
- •3.4. Выпуклость и вогнутость графика функции. Точки перегиба
- •3.5. Примерная схема построения графика функции
- •§ 4. Неопределенный интеграл
- •4.1. Первообразная функции и неопределенный интеграл
- •4.2. Основные свойства неопределенного интеграла
- •4.3. Таблица простейших неопределенных интегралов
- •4.4. Основные методы интегрирования
- •4.5. Проверка правильности нахождения неопределенного интеграла
- •§ 5. Определенный интеграл
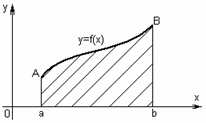
- •5.1. Понятие определенного интеграла
- •5.2. Основные свойства определенного интеграла
- •5.3. Формула Ньютона – Лейбница
- •5.4. Приложения определенного интеграла.
- •5.5. Биологические приложения определенного интеграла
- •1. Численность популяции.
- •2. Биомасса популяции.
- •3. Средняя длина пролета.
- •§ 6. Дифференциальные уравнения
- •6.1. Основные понятия и определения дифференциальных уравнений
- •6.2. Дифференциальные уравнения первого порядка. Задача Коши.
- •6.3. Дифференциальные уравнения первого порядка с разделенными и разделяющимися переменными
- •Глава 2. Теория вероятностей и математическая статистика
- •§ 1. Основные понятия и определения теории вероятностей.
- •1.1. Элементы комбинаторики.
- •1.2. Классическое определение вероятности
- •Основные свойства вероятности случайного события.
- •1.3. Теоремы сложения и умножения вероятностей .
- •1.4. Формула полной вероятности и формула Байеса
- •1.5. Повторные независимые испытания
- •§ 2. Случайные величины
- •2.1.Основные числовые характеристики дискретной случайной величины
- •§ 3. Математическая статистика.
- •§4. Элементы теории корреляции .
5.2. Основные свойства определенного интеграла
1. Определенный интеграл от алгебраической суммы нескольких функций, интегрируемых на отрезке , равен алгебраической сумме определенных интегралов этих функций на данном отрезке:
![]() .
.
2.
определенный интеграл от произведения
постоянного множителя
![]() на интегрируемую на отрезке
функцию
равен произведению этого множителя на
определенный интеграл от этой функции:
на интегрируемую на отрезке
функцию
равен произведению этого множителя на
определенный интеграл от этой функции:
![]() .
.
3. При перемене местами пределов интегрирования величина определенного интеграла изменяется на противоположную:
![]() .
.
4.
Если отрезок интегрирования
разбит точкой
![]() на два отрезка, то определенный интеграл
от функции
на отрезке
равен сумме определенных интегралов
от этой функции на каждом из этих
отрезков:
на два отрезка, то определенный интеграл
от функции
на отрезке
равен сумме определенных интегралов
от этой функции на каждом из этих
отрезков:
![]() .
.
5.3. Формула Ньютона – Лейбница
Теорема. Значение определенного интеграла равно разности значений любой первообразной от подынтегральной функции, взятой при верхнем и нижнем пределах интегрирования.
![]()
![]()
Данная формула называется формулой Ньютона – Лейбница и дает практически удобный метод вычисления определенного интеграла в том случае, когда известна первообразная подынтегральной функции.
Основными методами интегрирования определенного интеграла являются те же, что и для неопределенного.
Пример. Вычислить определенный интеграл
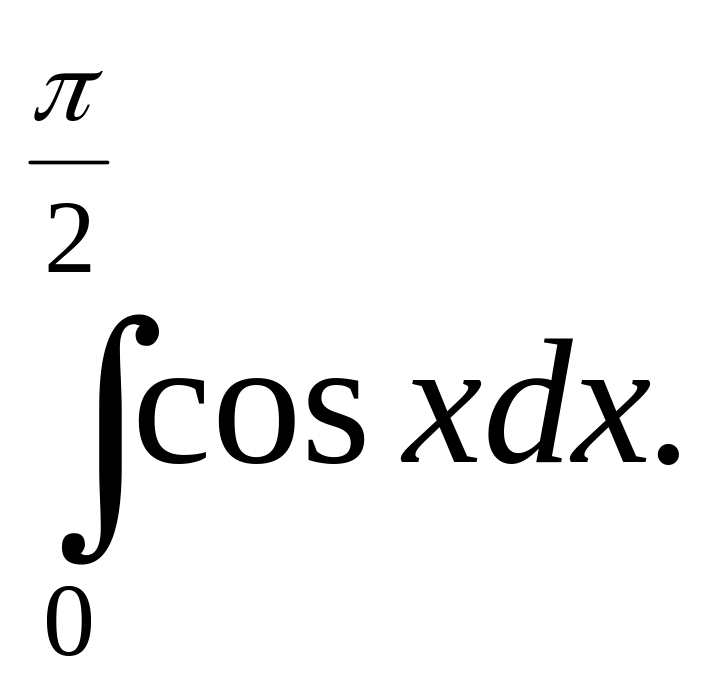
Решение.
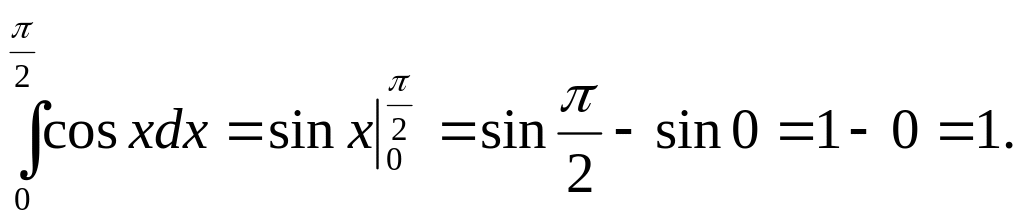
5.4. Приложения определенного интеграла.
1. Вычисление площадей плоских фигур.
а)
если непрерывная кривая задана
уравнением
,
где
![]()
|
![]()
б)
если непрерывная кривая задана уравнением
,
где
![]()
|
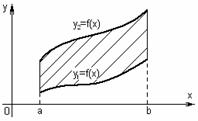
в)
если площадь ограничена двумя непрерывными
кривыми
![]() и
и
![]() ,
(
,
(![]() ),
прямыми
и
),
прямыми
и
|
Пример.
2. Объем тела вращения.
а) вокруг оси :
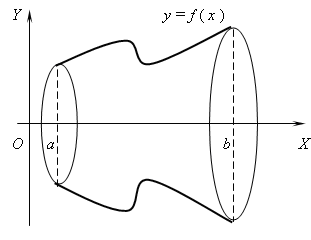
![]()
б)
вокруг оси
![]() :
:
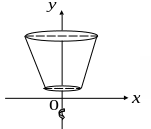
![]()
Пример.
5.5. Биологические приложения определенного интеграла
1. Численность популяции.
Число
особей в популяции (численность популяции)
меняется со временем. Если условия
существования популяции благоприятны,
то рождаемость превышает смертность и
общее число особей в популяции растет
со временем. Назовем скоростью роста
популяции прирост числа особей в единицу
времени. Обозначим эту скорость
![]() .
В
“старых”, установившихся популяциях,
давно обитающих в данной местности,
скорость роста
.
В
“старых”, установившихся популяциях,
давно обитающих в данной местности,
скорость роста
![]() мала
и медленно стремится к нулю. Но если
популяция молода, ее взаимоотношения
с другими местными популяциями еще
не установились или существуют внешние
причины, изменяющие эти взаимоотношения,
например сознательное вмешательство
человека, то
может значительно колебаться, уменьшаясь
или увеличиваясь.
мала
и медленно стремится к нулю. Но если
популяция молода, ее взаимоотношения
с другими местными популяциями еще
не установились или существуют внешние
причины, изменяющие эти взаимоотношения,
например сознательное вмешательство
человека, то
может значительно колебаться, уменьшаясь
или увеличиваясь.
Если
известна скорость роста популяции
,
то мы можем найти прирост численности
популяции за промежуток времени от
![]() до
до
![]() .
В
самом деле, из определения
следует, что эта функция является
производной от численности популяции
.
В
самом деле, из определения
следует, что эта функция является
производной от численности популяции
![]() в
момент
в
момент
![]() ,
и,
следовательно, численность популяции
является первообразной для
.
Поэтому
,
и,
следовательно, численность популяции
является первообразной для
.
Поэтому
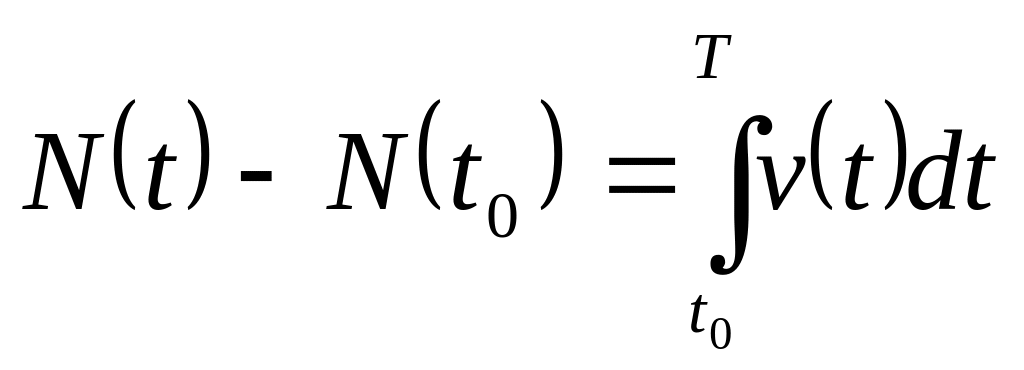 .
(1)
.
(1)
Известно,
что в условиях неограниченных
ресурсов питания скорость роста многих
популяций экспоненциальна, т. е.![]() .
Популяция
в этом случае как бы “не стареет”. Такие
условия можно создать, например, для
микроорганизмов, пересаживая время от
времени развивающуюся культуру в новые
емкости с питательной средой. Применяя
формулу (1), в этом случае получим:
.
Популяция
в этом случае как бы “не стареет”. Такие
условия можно создать, например, для
микроорганизмов, пересаживая время от
времени развивающуюся культуру в новые
емкости с питательной средой. Применяя
формулу (1), в этом случае получим:
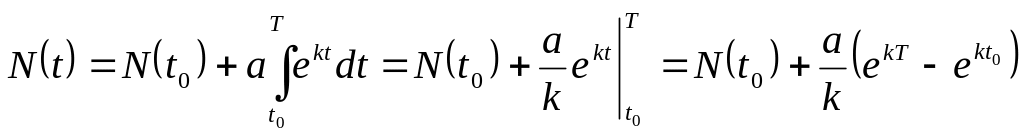
По данной формуле подсчитывают, в частности, численность культивируемых плесневых грибков, выделяющих пенициллин.