4.5. Проверка правильности нахождения неопределенного интеграла

Проверка правильности нахождения неопределенного интеграла основана на первом свойстве неопределенного интеграла, в соответствии с которым производная найденного неопределенного интеграла должна быть равна подынтегральной функции.

Следовательно, для проверки результата интегрирования достаточно найти производную этого результата и сравнить с подынтегральной функцией. В случае равенства производной и подынтегральной функции делается вывод о правильности нахождения неопределенного интеграла.

Пример. Вычислить следующий неопределенный интеграл и сделать проверку:

.

Решение:

Проверка: .

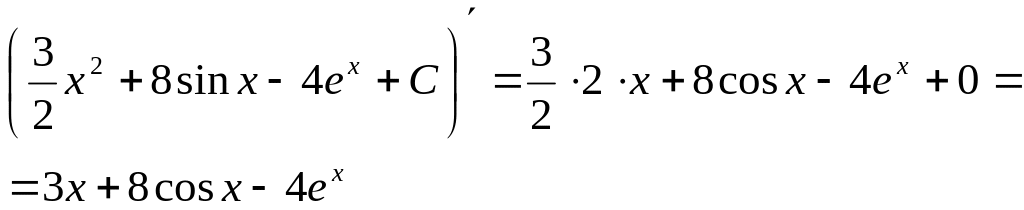§ 5. Определенный интеграл

Понятие определенного интеграла используют в ряде практических задач, в частности в задачах по вычислению площадей плоских фигур, объемов тел вращения, расчету работы, производимой переменной силой, нахождению численности популяции, биомассы популяции и т. д.

5.1. Понятие определенного интеграла

Определение. Фигура, ограниченная кривой , отрезком оси , прямыми и называется криволинейной трапецией.

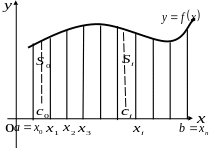
Для вычисления площади этой криволинейной трапеции разобьем отрезок произвольным образом на частей и обозначим точки деления , причем , а .

Восстановим из этих точек перпендикуляры до пересечения с кривой, получим значения функции в этих точках: . В результате этого площадь криволинейной трапеции окажется разбитой на сумму площадей элементарных криволинейных трапеций. В отрезках , , , , , возьмем совершенно произвольно точки и восстановим перпендикуляры из этих точек до пересечения с кривой . Получим значения .

Далее построим ступенчатую фигуру, состоящую из прямоугольников, имеющих своими основаниями отрезки , а высотами . Эта фигура ограниченна ломаной линией. Площадь этой ступенчатой фигуры можно считать приближенным значением площади заданной криволинейной трапеции, причем тем более точной, чем больше и чем меньше длины отрезков .

Площадь равна сумме площадей прямоугольников, построенных на отрезках:

(1)

Если теперь в (1) неограниченно увеличить число так чтобы длина наибольшего из отрезков стремилась к нулю, т. е. , то площадь криволинейной трапеции будет равна пределу суммы (1).

(2)

Сумма (1) называется интегральной суммой.

Определение. Если существует конечный предел интегральной суммы при условии, что , то этот предел называют определенным интегралом от функции на и обозначают .Т. об. По определению

Числа и называются нижним и верхним пределами интегрирования соответственно. Определенный интеграл выражает число.

Процесс вычисления определенного интеграла называют интегрированием. Функция называется подынтегральной функцией, а переменная – переменная интегрирования.

Определение. Функция называется интегрируемой на отрезке , если на этом отрезке существует определенный интеграл от этой функции.