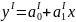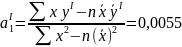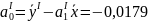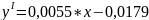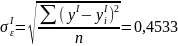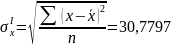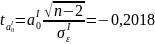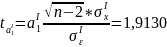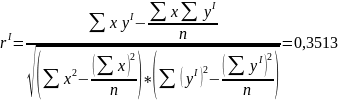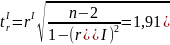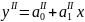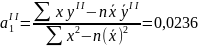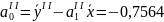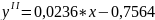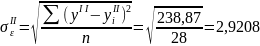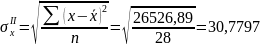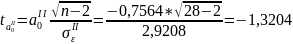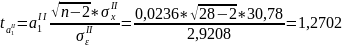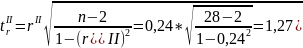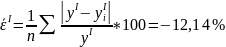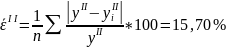2. Корреляционно-регрессионный анализ биржевой стоимости акций компании ial и Sears.

Постановка задачи.

Вариант №1.

Исследовать изменчивость биржевого рынка, используя модель простой линейной регрессии, считая зависимой переменной процентное изменение курсов анализируемых акций, а независимой переменной – процентное изменение рыночного индекса. В качестве рыночного индекса, как правило, применяется фондовый индекс 500 наиболее активно покупаемых акций на Нью-Йоркской фондовой бирже, публикуемый агентством Standard and Poor (S&P 500).

Таблица А.1 Динамика индекса S&P 500 и курсов акций компаний содержит данные, которые регистрировались каждую неделю с 14 мая 2012г. по 14 ноября 2012г. Недельные колебания индекса S&P 500 и курсов акций двух избранных компаний представляют собой процентное изменение по отношению к курсу акций на предыдущей неделе, зафиксированному на момент закрытия последних торгов. В Таблице А.1 содержатся значения следующих переменных: Неделя – текущая неделя; SP500 – недельное колебание индекса S&P 500; IAL - недельное колебание биржевой стоимости акций компании IAL; Sears - недельное колебание биржевой стоимости акций компании Sears.

По исходным данным таблицы Таблица А1.:

1. Постройте диаграмму разброса, считая, что зависимой переменной У является недельное колебание биржевой стоимости акций компании IAL (У1), а независимой Х – колебание индекса S&P 500.

2. Предполагая, что между переменными существует линейная зависимость, примените метод наименьших квадратов и вычислите параметры линейной зависимости а0 и а1. Расчеты выполнить по формулам. Результаты проверить с помощью Пакета анализа.

3. Объясните смысл полученных параметров.

4. Рассчитать теоретические уровни колебаний биржевой стоимости акций соответствующей компании по полученному уравнению регрессии.

5. Проверить параметры полученного уравнения регрессии на типичность с помощью t- критерия Стьюдента (для уровня значимости 0,05 или 5% и числа степеней свободы более 20 критическое значение t-критерия, полученное по таблице Стьюдента, равно 1,960).

6. Построить график полученного уравнения регрессии.

7. Оценить практическую значимость синтезированной модели с помощью линейного коэффициента корреляции.

8. Проверить существенность линейного коэффициента корреляции с помощью t- критерия Стьюдента (для уровня значимости 0,05 или 5% и числа степеней свободы более 20 критическое значение t-критерия, полученное по таблице Стьюдента, равно 1,960).

9. Повторите решение заданий 1-8, считая зависимой переменной У2 – недельное колебание биржевой стоимости акций компании Sears (У2).

10. Какая из составленных моделей наиболее адекватна? Для ответа исчислите средние ошибки аппроксимации каждой модели и сравните их между собой.

11. Вычислите линейный коэффициент корреляции для этих двух компаний.

12. Объясните смысл вычисленного коэффициента.

13. Целесообразно ли включать в портфель только акции компаний, связанных между собой сильной положительной корреляцией? Обоснуйте свой ответ, используя результаты вычисления линейного коэффициента корреляции.

14. Обобщив и сопоставив всю полученную информацию, сделайте практические выводы.

Решение

Произведем корреляционно-регрессионный анализ биржевой стоимости акций компании IAL.

Построим диаграмму разброса, считая, что зависимой переменной y^I является недельное колебание биржевой стоимости акций компании IAL , а независимой x – колебание индекса S&P 500 (см. рисунок 2.1)

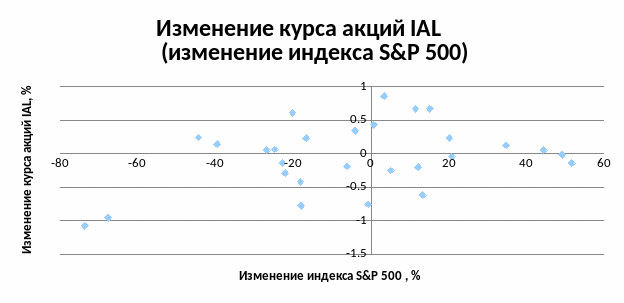
Рисунок 2.1 Диаграмма разброса курса акций компании IAL.

Произведем синтезирование адекватной экономико-математической модели в виде линейной зависимости:

( 2.1)

Для выполнения дальнейших расчетов построим вспомогательную таблицу А.2, куда занесем промежуточные расчеты.

Найдем параметры уравнения (2.1):

	( 2.0)
	( 2.0)

Полученная экономико-математическая модель примет вид:

( 2.0)

Проверим расчеты с помощью Пакета Анализа Excel (таблица А.3).

На рисунке 2.2 представим график уравнения регрессии (2.4).

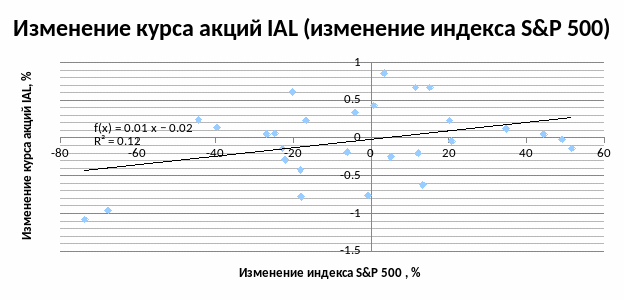
Рисунок 2.2 График уравнения линейной регрессии зависимости между курсом акций компании IAL и индексом S&P.

Проверим параметры полученного уравнения регрессии на типичность.

Найдем среднее квадратическое отклонение 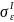и среднее квадратическое отклонение

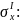
	( 2.0)
	( 2.0)

Вычислим значения t-критерия для параметров 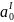и :

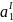( 2.0)

( 2.0)

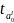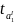Сравним значения и с критическим значением t_k = 1,960. Полученные в анализе корреляционной связи параметры уравнения регрессии являются нетипичными, т.к. не выполняется следующее условие: > t_k < .

Оценим практическую значимость синтезированной модели (с помощью линейного коэффициента корреляции ):

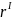( 2.0)

Значение больше нуля, следовательно, между изменением курса акций компании IAL и изменением индекса S&P существует прямо пропорциональная зависимость.

По шкале Чеддока установленная по уравнению (2.4) связь умеренная.

Оценим значимость (линейного коэффициента корреляции). Для этого определим фактическое значение критерия Стьюдена :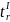

( 2.0)

Сравним рассчитанное значение критерия с критическим t_k = 1,960. Поскольку < t_k , то величина вычисленного линейного коэффициента корреляции признается не существенной.

Исчислим для проверки Пакета Анализа Excel (таблица 2.1).

Таблица 2.1 Линейный коэффициент корреляции .

	Изменение SP500	Изменение GM
Изменение SP500	1
Изменение GM	0,351260	1

Так как 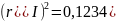, можно предположить, что 12,34% общей вариации курса акций компании IAL объясняется изменением индекса S&P.

Произведем аналогичным образом корреляционно-регрессионный анализ биржевой стоимости акций компании Sears.

Построим диаграмму разброса, считая, что зависимой переменной y^II является недельное колебание биржевой стоимости акций компании Sears , а независимой x – колебание индекса S&P 500 (см. рисунок 2.3).

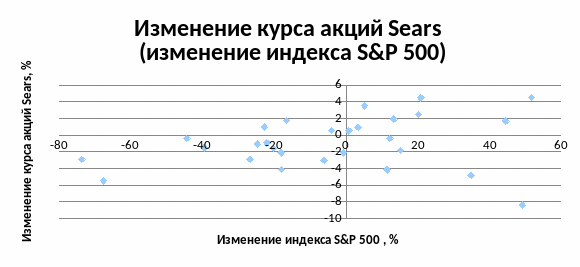
Рисунок 2.3 Диаграмма разброса курса акций компании Sears.

Произведем синтезирование адекватной экономико-математической модели в виде линейной зависимости.

( 2.01)

где , 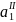- параметры уравнения.

Для выполнения расчетов построим вспомогательную таблицу А.4, куда занесем промежуточные расчеты.

Таблица А.4 Найдем параметры уравнения (2.11):

	( 2.10)
	( 2.10)

где n - число наблюдений (n=28).

Полученная экономико-математическая модель примет вид:

( 2.10)

Рассчитаем теоретические уровни колебаний биржевой стоимости акций компании Sears по полученному уравнению регрессии (таблица А.4, гр.6).

Проверим расчеты с помощью Пакета Анализа Excel (таблица А.5).

На рисунке 2.4 представим график уравнения линейной регрессии (2.14):

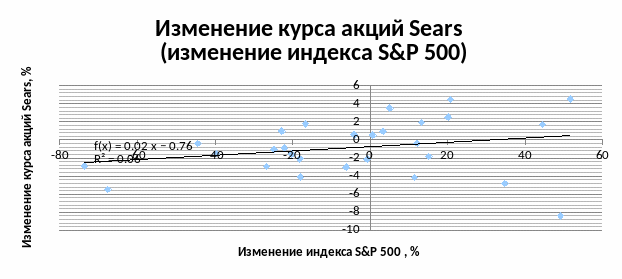
Рисунок 2.4 График уравнения линейной регрессии зависимости между курсом акций компании Sears и индексом S&P.

Проверим параметры полученного уравнения регрессии на типичность. Найдем среднее квадратическое отклонение 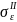и среднее квадратическое отклонение .

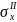	( 2.10)
	( 2.10)

Вычислим значения t-критерия для параметров 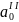и :

( 2.10)

( 2.10)

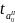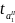Сравним значения и с критическим значением t_k = 1,960. Полученные в анализе корреляционной связи параметры уравнения регрессии являются нетипичными, т.к. не выполняется следующее условие: > t_k < .

Оценим практическую значимость синтезированной модели (с помощью линейного коэффициента корреляции ):

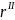( 2.10)

Значение 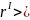0, следовательно, между изменением курса акций компании Sears и изменением индекса S&P существует прямо пропорциональная зависимость.

Линейный коэффициент корреляции предназначен для расчета силы и направления линейной зависимости между переменными исследования. Он отражает меру линейной зависимости между двумя переменными.

Положительное значение коэффициента корреляции соответствует возрастающей зависимости, отрицательное – убывающей. При нулевом значении коэффициента корреляция взаимосвязь отсутствует. 

По шкале Чеддока установленная по уравнению (2.14) связь слабая.

Оценим значимость линейного коэффициента корреляции. Для этого определим фактическое значение критерия Стьюдента :

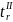( 2.20)

Сравним рассчитанное значение критерия с критическим t_k = 1,960. Поскольку < t_k , то величина вычисленного линейного коэффициента корреляции признается не существенной.

Исчислим для проверки Пакета Анализа Excel (таблица 2.2).

Таблица 2.2 Линейный коэффициент корреляции .

	Изменение SP500	Изменение Sears
Изменение SP500	1
Изменение Sears	0,241723	1

Так как 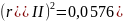, можно предположить, что 5,76% общей вариации курса акций компании Sears объясняется изменением индекса S&P.

Исследуем на адекватность уравнения регрессии моделей (2.4) и (2.14).

Средняя ошибка аппроксимации для модели (2.4) (компания IAL) :

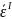( 2.21)

Средняя ошибка аппроксимации для модели (2.14) (компания Sears) :

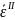( 2.22)

Допустимый предел значений средней ошибки аппроксимации не должен превышать 8-10% . Значение средней ошибки аппроксимации и превышают допустимое значение, следовательно, уравнения (2.4) и (2.14) не желательно использовать в качестве регрессии.

Сравнивая значения средних ошибок аппроксимации двух моделей, можно сказать, что математическая модель (2.4) (компания IAL) является более адекватной для практических целей, чем математическая модель (2.14) (компания Sears) так как > .