МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Институт бизнеса и менеджмента технологий

КУРСОВАЯ РАБОТА

на тему: Применение статистических методов анализа в бизнесе

Студент

2 курса

группы 2311 А.С.Гринаш

Руководитель

старший преподаватель Е.А.Гопка

Минск – 2014

Содержание

Y

КУРСОВАЯ РАБОТА 1

Введение 3

1. Теоретические основы корреляционно-регрессионного анализа 4

2. Корреляционно-регрессионный анализ биржевой стоимости акций компании ial и Sears. 7

Заключение 16

Список использованных источников 18

Введение

В наше время математико-статистические исследования становятся необходимым инструментом для получения более глубоких и полноценных знаний о механизме изучаемых явлений. Существующие между явлениями формы и виды связей весьма разнообразны по своей классификации, но предметом статистики являются только такие из них, которые имеют количественный характер и изучаются с помощью количественных методом. Основным в изучении взаимосвязей явлений, является метод корреляционно-регрессивного анализа. Обработка статистических данных уже давно применяется в самых разнообразных видах человеческой деятельности.

Целью курсовой работы является использование теоретических знаний статистических методов анализа для развития практических умений и навыков в конкретных ситуациях, связанных с ведением бизнеса.

Задачей исследования состоит в изучении статистических методов анализа и применении корреляционно-регрессионного метода анализа для определения характера модели изменчивости биржевого рынка.

В ходе выполнения курсовой работы изучаются теоретические основы и практическое применение корреляционно-регрессионного метода статистического анализа.

1. Теоретические основы корреляционно-регрессионного анализа

Корреляционно-регрессионный анализ как общее понятие включает в себя измерение тесноты, направления связи и установление аналитического выражения (формы) связи (регрессионный анализ). Этот метод содержит две составляющие части – корреляционный анализ и регрессионный анализ.

Корреляционный анализ – это количественный метод определения тесноты и направления взаимосвязи между выборочными переменными величинами. Теснота связи количественно выражается величиной коэффициента корреляции. Знак при коэффициенте корреляции характеризует направление связи между признаками. Основными задачами корреляционного анализа являются оценка силы связи и проверка статистических гипотез о наличии и силе корреляционной связи. Не все факторы, влияющие на экономические процессы, являются случайными величинами, поэтому при анализе экономических явлений обычно рассматриваются связи между случайными и неслучайными величинами. Такие связи называются регрессионными, а метод математической статистики, их изучающий, называется регрессионным анализом.

В статистике принято различать следующие варианты зависимостей:

1. Парная корреляция – связь между двумя признаками (результативным и факторным или двумя факторными).

1. Частная корреляция – зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков.

2. Множественная корреляция – зависимость результативного и двух или более факторных признаков, включенных в исследование.

Относительно формы связи различают:

А) линейную корреляцию – характеризует тесноту и направление связи между двумя коррелируемыми признаками, в случае наличия между ними линейной зависимости.

Б) нелинейную – корреляция, при которой отношение степени изменения одной переменной к степени изменения другой переменной является изменяющейся величиной.

Регрессионный анализ – заключается в определении аналитического выражения связи, в котором изменение одной величины обусловлено влиянием одной или нескольких величин, а множество всех прочих факторов, также оказывающих влияние на зависимую величину, принимается за постоянные и средние значения. Регрессия может быть однофакторной(парной) и многофакторной(множественной).

Относительно формы зависимости различают:

А) линейную регрессию, выражаемую линейной функцией. При этой форме зависимости между исследуемыми переменными объективно существуют линейные соотношения. Выражается уравнением прямой вида:

Б) нелинейную регрессию, выражаемую нелинейной функцией. В этом случае между исследуемыми экономическими явлениями объективно существуют нелинейные соотношения. Выражается уравнением вида:

Парабола –

Гипербола –

По направлению связи различают:

1) прямую регрессию(положительную), возникающую при условии, если с увеличением или уменьшением независимой величины значения зависимой также соответственно увеличиваются или уменьшаются;

2) обратную(отрицательную) регрессию, появляющуюся при условии, что с увеличением или уменьшением независимой величины зависимая соответственно уменьшается или увеличивается.

Модели, построенные по данным первого типа, называются пространственными моделями. Модели, построенные на основе второго типа данных, называются моделями временных рядов[1].

Рассмотрим теперь вопрос оценки качества статистической связи. Мерой оценки силы статистической зависимости между показателями Х и Y служит коэффициент корреляции Пирсона r. [2., c. 182]

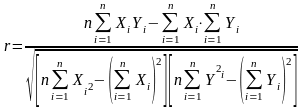
Коэффициент корреляции Пирсона r обладает следующими свойствами:

1. Коэффициент корреляции изменяется в пределах -1≤ r ≤1.

2. Модуль коэффициента корреляции характеризует силу статистической связи, чем больше |r |, тем сильнее связь, в частности если r = ±1, то связь функциональная, если r близок к нулю, то связь слабая или отсутствует.

3. Знак коэффициента корреляции характеризует направление статистической связи, если r > 0, то с ростом Х показатель Y также растет, если r < 0 , то с ростом Х показатель Y убывает.

4. Величина R = r² называется коэффициентом детерминации, его можно интерпретировать как среднюю долю влияния показателя Х на Y.

Для ответа на вопрос: можно ли считать связь между показателями достаточно сильной, чтобы считать Х и Y зависимыми и уравнение их регрессии имеет смысл, используется методика проверки значимости коэффициента корреляции.