Тема 2 геометрические построения

1.1. Построение параллельных прямых

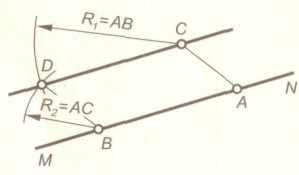И меется прямая MN (рис. 1.1) и точка С, не лежащая на этой прямой. Требуется через точку С провести прямую, парал­лельную прямой МN.

Н

Рис. 1.1

а прямой MN следует выделить произвольный отрезок АВ. Из точки С, как из центра, провести дугу окружности радиусом R₁, равным отрезку АВ, а из точки В дугу окружности радиусом R₁, равным отрезку АС. Пересечение двух дуг в точке О позволит провести прямую СD параллельную прямой МN.

1.2. Построение взаимно перпендикулярных прямых

Имеется прямая АВ (рис. 1.3) и принадлежащая ей точ­ка С. Требуется провести через точку С прямую, перпендикуляр­ную к прямой АВ.

И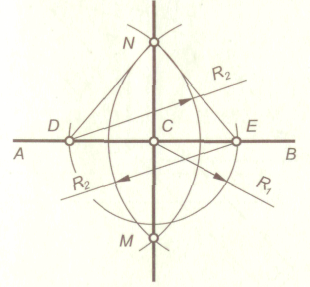

Рис. 1.3

з точки С дугой окружности произвольным радиусом R₁ следует отложить на прямой АВ два равных отрезка: СD и СЕ. Из точек О и Е, как из центров, провести две дуги окружностей с радиусом R₂, раз­мер которого выбирается несколько больше, чем длина отрезка СО = СЕ. Пересечение дуг в точке N позволяет провести перпендику­ляр СN к прямой АВ. Вторая точка пересечения этих дуг — точка М может служить для контроля точности построения.

Имеется прямая АВ (рис. 1.5) и не принадлежащая ей точ­ка С. Требуется провести через точку С прямую, перпендикуляр­ную к прямой АВ.

И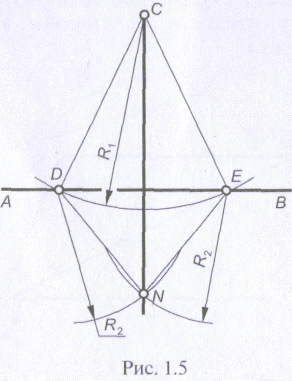 з точки С, как из центра, проводят дугу окружности радиу­сом R₁. Размер радиуса выбирается несколько больше, чем рассто­яние от точки С до прямой АВ. Пересечение дуги с прямой АВ определяет положение точек D и Е. Из точек D и Е, как из цент­ров, проводят дуги окружностей с произвольным радиусом R₂. Пересечение этих дуг дает точку N, которую соединяют с точкой С. Отрезок СN — искомый перпендикуляр к прямой АВ.

1.3. Деление отрезка прямой

П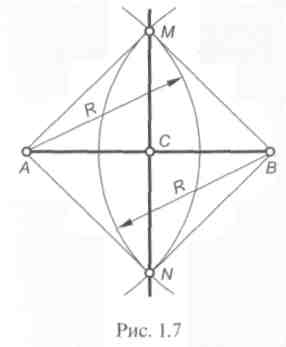 усть необходимо разделить отрезок АВ (рис. 1.7) пополам. Из концов А и В отрезка, как из центров, провести дуги ок­ружностей радиусом R, размер которого должен быть несколько больше, чем половина длины отрезка АВ, и точки M и N пересечения дуг соединить прямой. Точка С пересечения прямой МN с прямой АВ разделит заданный отрезок пополам.

1.4. Построение углов

Пусть угол AВС (рис. 1.12), равный α, необходимо разделить пополам.

И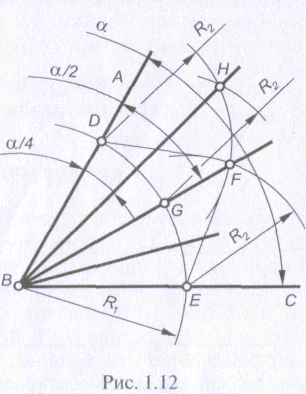 з вершины угла В, как из центра, провести дугу окружности произвольным радиусом R₁, которая пересечет стороны угла в точ­ках D и Е. Из этих точек, как из центров, надо провести дуги окружностей произвольным радиусом R₂, пересечение которых в точке F даст возможность провести биссектрису ВF угла AВС и получить углы АВF и FВС, равные α/2.

1.5. Деление окружности на равные части, построение правильных многоугольников Деление окружности на 4 и 8 частей

К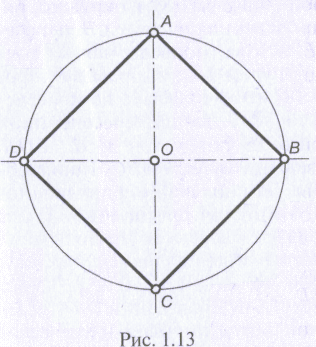 онцы взаимно перпендикулярных диаметров АС и ВD (рис. 1.13) делят окружность с центром в точке О на 4 равные части. Соеди­нив концы этих диаметров, можно получить квадрат АВСD.

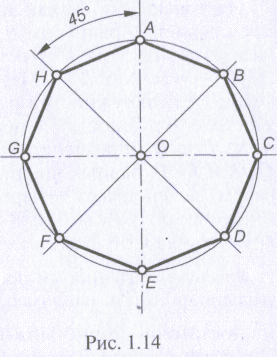
Если угол СОА между взаимно перпендикулярными диаметрами АЕ и СG (рис. 1.14) разделить пополам и провести взаимно перпен­дикулярные диаметры ОН и ВР, то их концы разделят окружность с центром в точке О на 8 равных частей. Соединив концы этих диамет­ров, можно получить правильный восьмиугольник АВСDЕFGН.