Рівняння Хілла. Потужність одиночного скорочення

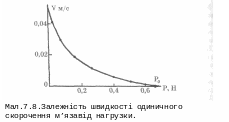
Залежність швидкості укорочення від навантаження Р є найважливішою при вивченні роботи м'яза, тому що дозволяє виявити закономірності м'язового скорочення і його енергетиків. Вона була докладно вивчена при різних режимах скорочення Хіллом і представлена на мал. 7.8.

Їм же було запропоновано емпіричне вираження, що описує цю криву:

(7.2)

Цей вираз називається рівнянням Хілла і є основним характеристичним рівнянням механіки м'язового скорочення. Ρ₀ - максимальна ізометрична напруга, що розвивається м'язом, або максимальний вантаж, утримуваний м'язом без її подовження; b - константа, що має розмірність швидкості, а - константа, що має розмірність сили.

З рівняння (7.2) випливає, що максимальна швидкість розвивається при Ρ = 0:

При Ρ = Р₀ одержуємо V = 0, тобто укорочення не відбувається.

Робота А, вироблена м'язом при одиночному укороченні на величину Δl дорівнює:

А = Pl.

Ця залежність, мабуть, нелінійна, тому що V = f (P). Але на ранній фазі скорочення можна зневажити цією нелінійністю і вважати V = const. Тоді

l = Vt,

а потужність, що розвивається м'язом, має вигляд:

W = PV (7.3)

Підставляючи (7.2) у (7.3), одержимо залежність потужності від сили, що розвивається, Р:

Функція W (Ρ) має колоколовидну форму і представлена на мал. 7.9.

Ц я крива, отримана з рівняння Хілла, добре погодиться з результатами досвідів. Потужність дорівнює нулеві при Р = Р₀ і Р = 0 і досягає максимального значення при оптимальній величині навантаження Ρ_опт:

тобто коли Ρ = 0,31 P₀.

Е фективність роботи м'яза при скороченні може бути визначена як відношення зробленої роботи до витраченої енергії ΔΕ:

.

Розвиток найбільшої потужності й ефективності скорочення досягається при зусиллях 0,3 - 0,4 від максимального ізометричного навантаження Р₀ для даного м'яза. Це використовують, наприклад, спортсмени-велогонщики: при переході з рівнини на гірську ділянку навантаження на м'язи зростає і спортсмен переключає швидкість на нижчу передачу, тим самим зменшуючи Р, наближаючи неї до Р_опт.

Практично ефективність може досягати значень 40-60 % для різних типів м'язів. Найвища ефективність спостерігається в м'язів черепахи, що досягає 75-80 %.

Моделювання м'язового скорочення

Рівняння (7.2) було отримано при узагальненні великої кількості досвідчених даних. Вид цього рівняння вказує на існування в м'язі внутрішнього грузлого (залежного від швидкості) тертя, що перешкоджає її укороченню. Однак природа цього, як і фізичний зміст констант а і b, залишалися не ясними. Пояснення цих і ряду інших явищ були дані в математичній моделі скорочення м'яза, запропонованої В.Дещеревським, на моделі ковзних ниток (див. § 25).

Передбачається, що сила скорочення волокна дорівнює сумі сил, генерованих містками в шарі, рівному половині саркомера, тому що саркомери по товщині волокна включені паралельно. Швидкість зміни довжини волокна V_в:

V_в = 2NV*,

д е N - число саркомерів у волокні, V* - відносна швидкість ковзання ниток. При ковзанні ниток місток може знаходитися в одному з трьох можливих станів: розімкнуте, замкнуте що тягне - коли голівка генерує силу +f, спрямовану до центра саркомера, і замкнуте гальмуюче - коли актинова нитка пройшла координату центра прикріплення голівки і прикріплений місток створює негативну по на прямку силу - f, після чого він розмикається.

Переходи з одного стану в інше, представлені на мал. 7.10, визначаються відповідними константами швидкостей. Повний цикл містка супроводжується розпадом молекул АТФ.

Д ля загального числа що тягнуть (х) і гальмують (z) містків що розвивається саркомером сила F:

F = xf – zf.

Очевидно, що перший доданок - це сила, генеруюча замкнутими, а друге - гальмуючими містками. Тоді система кінетичних диференціальних рівнянь для станів містків може бути записана у виді:

(7.4, а)

(7.4, б)

(7.4, в)

де а(l) - число містків, здатних замикатися при довжині 0,5 саркомера в шарі волокна товщиною l, Μ - маса навантаження, Ρ - сила, що розвивається волокном.

Зміст кінетичних рівнянь (7.4, а, б, в) досить ясний. Наприклад, у рівнянні (7.4, а) ліва частина - швидкість зміни кількості містків, що тягнуть. У правій частині перший доданок а(l) - загальне число містків мінус кількість що тягнуть x і гальмують z містків, тобто в квадратних дужках - кількість розімкнутих містків, що залишилися. Множачи цю кількість на константу k₁, одержуємо швидкість збільшення кількості містків, що тягнуть, (верхня стрілка на мал. 7.10); другий доданок - швидкість зменшення кількості містків, що тягнуть, за рахунок їхнього переходу в гальмуючий стан (права стрілка мал. 7.10). Різниця між швидкостями росту й убування кількості містків, що тягнуть, дає шукану швидкість зміни їхньої кількості. Рівняння (7.4, б) і (7.4, в) записуються аналогічно.

При ізотонічному скороченні з постійною швидкістю в області з постійним числом містком (стан б на мал. 7.3) a(l) = a₀ – максимальному числу містків, що можуть брати участь у скороченні.

У цьому випадку значення величин x, z і U не міняються в часі, тобто система знаходиться в стаціонарному стані:

(7.5)

Тоді із системи рівнянь (7.4 а, б, в) і умови стаціонарності (7.5) одержуємо:

(7.6 а)

(7.6 б)

(7.6 в)

Вираження для стаціонарної швидкості укорочення (7.6 в) збігається з рівнянням Хілла (7.2). При цьому:

(7.7)

Тобто, якщо вираження (7.7) підставити в рівняння (7.6, в) для швидкості U_ст, то виходить рівняння (7.2).

Таким чином, кінетична модель Дещеревського дозволила пояснити феноменологічне рівняння Хілла, зміст констант а і b, що входять у нього, зміст величини максимальної сили Р₀ ізометричного скорочення. Крім того, показано, що внутрішній грузлий компонент м'яза визначається силою, що розвивається гальмуючими містками, число яких росте зі збільшенням швидкості скорочення м'яза (7.7).

Виходячи з даних електронної мікроскопії, рентгеноструктурного аналізу і запропонованої моделі, було розраховано, що на одну нитку актину приходиться зусилля 3  10^-10 Η при максимальному ізометричному навантаженні Ρ₀ = 30 Η / см². Вважаючи, що в кожній структурній одиниці знаходиться 1 молекула міозину і за кожен цикл замикання-розмикання розщеплюється 1 молекула АТФ, енергія якої використовується на 50 %, отримані наступні характеристики одиничного елемента: f = 3  10^-12 Н,  = 10^-8 м = 10 нм, енергія скорочення Ε = 6  10^-20 Дж, час замикання 1 мс. У такий спосіб сила, генеруюча одиничним елементом, лише в 3 рази перевищує силу тяжіння двох мас 1 м на відстані 1 мм, рівну 10^-12 Н. Цілий же м'яз може розвивати силу до 10⁴ Η (до 1 тонни), тобто на 16 порядків більше!