5 Моделирование систем массового обслуживания

5.1 Аналитические модели систем массового обслуживания

5.1.1 Потоки событий

Потоком событий называется последовательность однородных собы­тий, появляющихся одно за другим в случайные моменты времени. При­меры: поток вызовов на телефонной станции; поток сбоев ЭВМ; поток заявок на проведение расчетов в вычислительном центре и т.п.

Поток событий наглядно изображается рядом точек с абсциссами Q_1, Q₂, ..., Q_n, ... (рис. 5.1) с интервалами между ними: Т₁ = Q₂ - Q_1, T₂ = Q₃ -Q₂, ..., Т_п = Q_n+1 - Q_n. При его вероятностном описании поток событий может быть представлен как последовательность случайных ве­личин: Q₁; Q₂ = Q₁ + T₁; Q₃ = Q₁ + T₁ + T₂; и т.д. На рисунке в виде ряда точек изображен не сам поток событий (он случаен), а только одна его конкретная реа­лизация.

Ранее упоминалось о потоках событий и некоторых их свойствах; здесь рассмотрим их более подробно. Поток событий называется стационар­ным, если его вероятностные характеристики не зависят от выбора начала отсчета или, более конкретно, если вероятность попадания того или другого числа событий на любой интервал времени зависит только от длины этого интервала и не зависит от того, где именно на оси 0-t он расположен.

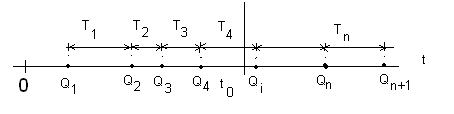
Рисунок 5.1 – Реализация потока событий

Поток событий называется ординарным, если вероятность попадания на элементарный интервал времени двух или более событий пренебре­жимо мала по сравнению с вероятностью попадания одного события.

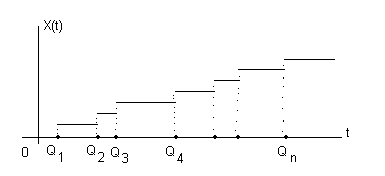
Рисунок 5.2 – Поток событий как случайный процесс

Ординарный поток событий можно интерпретировать как случайный процесс Х(t) - число событий, появившихся до момента t (рис. 5.2). Случайный процесс Х(t) скачкообразно возрастает на одну единицу в точках Q ,Q₂ ,...,Q _n.

Поток событий называется потоком без последействия, если число собы­тий, попадающих на любой интервал времени , не зависит от того, сколь­ко событий попало на любой другой не пересекающийся с ним интервал. Практически отсутствие последействия в потоке означает, что события, образующие поток, появляются в те или другие моменты времени незави­симо друг от друга.

Поток событий называется простейшим, если он стационарен, ордина­рен и не имеет последействия. Интервал времени T между двумя соседними событиями простейшего потока имеет показательное распределение

(при t>0) ; (5.1)

где / М [Т] - величина, обратная среднему значению интервала Т.

Ординарный поток событий без последствия называется пуассоновским. Простейший поток является частным случаем стационарного пуассоновского потока. Интенсивностью потока событий называется среднее число событий, приходящееся на единицу времени. Для стационарного потока ; для нестационарного потока она в общем случае зависит от времени: .

Мгновенная интенсивность потока (t) определяется как предел отно­шения среднего числа событий, которые произошли за элементарный ин­тервал времени , к длине этого интервала, когда она стремит­ся к нулю. Среднее число событий, наступающих на интервале времени τ, следующем непосредственно за моментом t₀ (см. рис. 5.1), равно

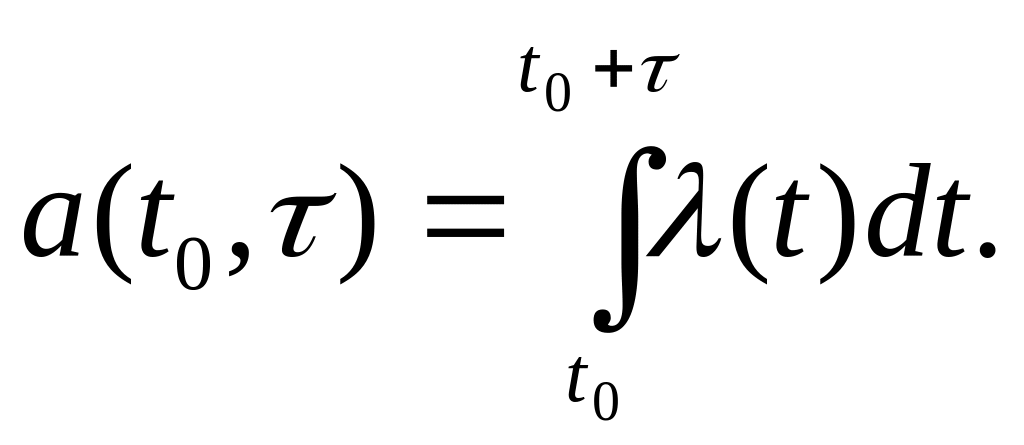
Если поток событий стационарный, то

Ординарный поток событий называется потоком Пальма (рекуррентным потоком, или потоком с ограниченным последствием), если интервалы времени Т_1,Т₂,... между событиями (см. рис.5.1) представляют собой независимые, одинаково распределенные случайные величины. В связи с одинаковостью распределений Т_1, Т₂, ... поток Пальма всегда стационарен. Простейший поток является частным случаем потока Пальма; в нем интервалы между событиями распределены по показательному закону (5.1), где λ - интенсивность потока.

Потоком Эрланга k-го порядка называется поток событий, получаю­щийся «прореживанием» простейшего потока, когда сохраняется каждая k-я точка (событие) в потоке, а все промежуточные выбрасываются (на рис. 5.3 показано получение потока Эрланга 4-го порядка из простей­шего потока).

Интервал времени между двумя соседними событиями в потоке Эр­ланга к - го порядка представляет собой сумму k независимых случайных величин T₁, Т₂, ..., Т_k имеющих показательное распределение с парамет­ром :

. (5.2)

Закон распределения случайной величины Т называется законом Эр­ланга k-го порядка и имеет плотность

(при t >0). (5.3)

Математическое ожидание, дисперсия и среднеквадратичное от­клонение случайной величины Т (5.2) соответственно равны:

. (5.4)

Коэффициент вариации случайной величины (5.2) равен

(5.5)

При увеличении порядка потока Эрланга «степень случайности» интервала между событиями стремится к нулю.

Если одновременно с «прореживанием» простейшего потока изме­нять масштаб по оси 0-t (делением на k), получится нормированный поток Эрланга k-го порядка, интенсив­ность которого не зависит от k.

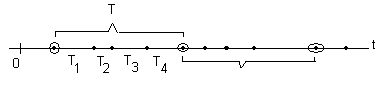
Рис.5.3

Числовые характеристики случайной величины в нормированном потоке Эрланга k-го порядка равны:

При увеличении k нормированный поток Эрланга неограниченно при­ближается к регулярному потоку с постоянным интервалом I = 1 / меж­ду событиями.