§12. Основные теоремы дифференциального исчисления

Теорема 1 (Ферма, фр., 1601-1665). Пусть функция y=f(x) определена на некотором промежутке <a;b> и в некоторой точке x₀<a;b> имеет наименьшее или наибольшее значение. Тогда если функция дифференцируема в точке x₀, то f (x₀)=0.

Доказательство.

Пусть f(x₀) – наибольшее значение функции f(x) на <a;b>. Тогда по определению x<a;b> выполнено f(x)≤ f(x₀).

Если x< x₀, то ; если x> x₀, то .

По условию  f (x₀), то есть  f (x₀+0),  f (x₀-0) и f (x₀+0)= f (x₀-0)=f (x₀).

Тогда по теореме о предельном переходе в неравенствах ,

.

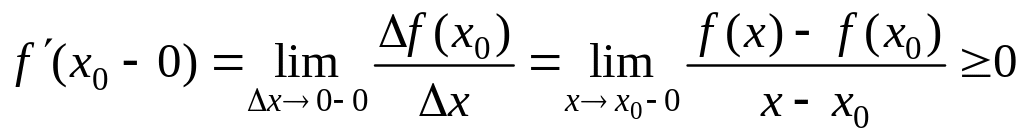Из того, что следует, что f (x₀)=0.

А налогично рассматривается случай, когда f(x₀) – наименьшее значение функции.

Геометрический смысл. Если функция f, дифференцируемая в точке x₀, имеет в ней наименьшее или наибольшее значение, то в точке (x₀;f(x₀)) касательная к графику функции f(x) параллельна оси Ох.

Замечание. Теорема не верна, если x₀ – один из концов отрезка [a;b].

Рассмотрим, например, f(x)=x. В точке а – наименьшее значение, в точке b – наибольшее, но .

Важно также условие дифференцируемости функции.

Рассмотрим, например, y=|x|. В точке x₀=0- наименьшее значение, но f (x₀)0 (f (x₀) не существует).

Теорема 2 (Ролля, фр., 1672-1719). Пусть функция f(x) определена на [a;b], причем

1. f(x)C[a;b],

2. f(x) дифференцируема на (a;b),

3. f(a)= f(b).

Тогда существует точка с(a;b), такая что f (c)=0.

Доказательство.

Так как f(x) непрерывна на [a;b], то она имеет наименьшее значение, равное m и наибольшее значение, равное М (по 2-й теореме Вейерштрасса), то есть x[a;b] выполнено m≤ f(x)≤M.

1. Если m=M, то f(x)=М x[a;b]. Следовательно, f (x)=0 и, значит, в качестве точки с можно взять любую точку из (a;b).

2. Пусть mM, m<M.

 одно из чисел m или M отлично от f(a). Пусть Mf(a), Mf(b). Т. к. f – непрерывная функция, то по 2-й теореме Вейерштрасса существует точка с[a;b], такая что f (c)=М. Она может быть только внутренней точкой, т. к. из того, что Mf(a)  са, а из того, что Mf(b)  сb  с(a;b).

Т. о., f имеет наибольшее значение в некоторой внутренней точке с(a;b), f дифференцируема в точке с, следовательно, по теореме Ферма f (c)=0.

Геометрический смысл. У графика непрерывной на [a;b] и дифференцируемой на (a;b) функции f(x), принимающей на концах отрезка [a;b] равные значения, существует точка, в которой касательная параллельна оси Ох (таких точек может быть несколько, могут быть и все точки интервала, если m=M (f(x)=с)).

Замечание. Если f(a)= f(b)=0 и выполнены условия теоремы Ролля, то  с(a;b): f (c)=0. То есть между двумя нулями дифференцируемой функции лежит, по крайней мере, один нуль ее производной.

Теорема 3 (Лагранжа, фр., 1736-1813, теорема о конечных приращениях). Пусть функция f(x) определена на [a;b], причем

1. f(x)C[a;b],

2. f(x) дифференцируема на (a;b).

Тогда существует точка с(a;b), такая что . (1)

Доказательство.

Рассмотрим на [a;b] вспомогательную функцию

.

Она удовлетворяет условиям теоремы Ролля:

1. (х) непрерывна на [a;b] как разность непрерывной функции f(x) и линейной функции;

2.   (х) х(a;b);

3. (b)=f(b)-f(a)-(f(b)-f(a))=0; (a)=f(a)-f(a)=0  (a)=(b).

С ледовательно, по теореме Ролля  с(a;b):  (c)=0, т. е.

 .

Формула (1) называется формулой Лагранжа. Ее другая форма записи:

f(b)-f(a)=f(c)(b-a). (2)

Геометрический смысл.

, k_кас.=f (c),

 k_кас.=k_сек.

На графике существует точка (с;f(c)), касательная в которой параллельна секущей, проходящей через точки (a;f(a)), (b;f(b)).

П ример. На кривой f(x)=4-x² найти точки, в которых касательная параллельна хорде, соединяющей точки (-1;3) и (2;0).

 f(x)=4-x², [a;b]=[-1;2], выполнены условия теоремы Лагранжа. Следовательно, существует точка с(-1;2), такая что .

f (х)=-2х  , -2с=-1, с=0,5. 

Замечание 1. Теорема Ролля является частным случаем теоремы Лагранжа, когда f(a)=f(b).

З амечание 2. Пусть a<b. с(a;b) выполнено , 0<<1  c=a+(b-a), 0<<1.

Если a>b, с(a;b) выполнено , 0<<1   c=a+(b-a), 0<<1.

Тогда формула (2) примет вид

f(b)-f(a)=f (a+(b-a))(b-a), 0<<1. (2)

Замечание 3. Пусть функция f удовлетворяет условиям теоремы Лагранжа на [a;b]. Произвольному значению x[a;b] придадим приращение x, так, что x+x[a;b]. Рассмотрим [x;x+x], если x>0 и [x+x;x], если x<0. На этом отрезке функция удовлетворяет условиям теоремы Лагранжа. Следовательно,

f(x+x)-f(x)=f (c) x= f (x+x)x, 0<<1,

f(x)=f (x+x)x. (3)

Формула (3) называется формулой конечных приращений (это тоже формула Лагранжа). Из (3) следует, что если x конечно, то и f(x) конечно.

Если сравнить (3) с приближенной формулой f(x)f (x)x, x0, то видно, что при отбрасывании слагаемого (x) x в f(x) все-таки можно сохранить знак равенства, но для этого надо брать значение производной не в точке х, а в некоторой точке x+x, заключенной между х и x+x. Правда, это значение неизвестно, а установлен только факт его существования. Но это часто используется.

Теорема 4 (Коши, обобщенная теорема о конечных приращениях). Пусть на [a;b] определены функции f(x) и g(x), причем

1. f(x), g(x)C[a;b],

2. f(x), g(x) дифференцируемы на (a;b),

3. g (x)0 х(a;b).

Тогда существует точка с(a;b), такая что . (4)

Доказательство.

Левая часть равенства (4) имеет смысл, т. к. выполнено условие 3). Действительно, если бы g(b)=g(a), то к функции g(x)можно было бы применить теорему Ролля, и оказалось бы, что , но это противоречит условию 3). Следовательно, g(b)g(a) и формула (4) имеет смысл.

Рассмотрим вспомогательную функцию

.

Эта функция удовлетворяет на [a;b] условиям теоремы Ролля:

1. (х) непрерывна на [a;b] как линейная комбинация непрерывных функций,

2. (х) дифференцируема на (a;b): ;

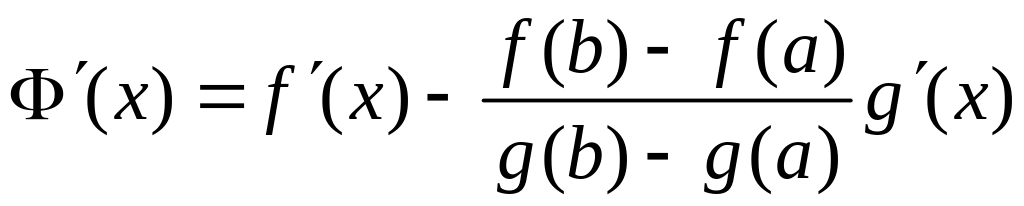3. (a)=0, (b)=0, т. е. (a)=(b).

По теореме Ролля

 .

Замечание. Теорема Лагранжа является частным случаем теоремы Коши при g(x)=x.

Теоремы Ролля, Лагранжа, Коши часто называют теоремами о средних значениях, т. к. в них речь идет о производных при каких-то средних значениях независимой переменной. В теоремах установлен лишь факт существования этих значений. Иногда их можно вычислить.