§ 16. Асимптоты графика функции

Определение 1. Прямая х=а называется вертикальной асимптотой графика функции f(x), если хотя бы один из односторонних пределов функции в точке а равен + или -.

Пример.  х=0 – вертикальная асимптота графика функции : , . 

Определение 2. Пусть f(x) определена x>a (x<a), . Прямая y=kx+b называется наклонной асимптотой графика функции f(x) при х+ (х-), если f(x)=kx+b+(х), где .

При k0 y=kx+b – наклонная асимптота, при k=0 прямая y=b – горизонтальная асимптота.

Теорема. Для того, чтобы прямая y=kx+b являлась наклонной асимптотой графика функции f(x) при х+ (х-), необходимо и достаточно, чтобы существовали 2 конечных предела:

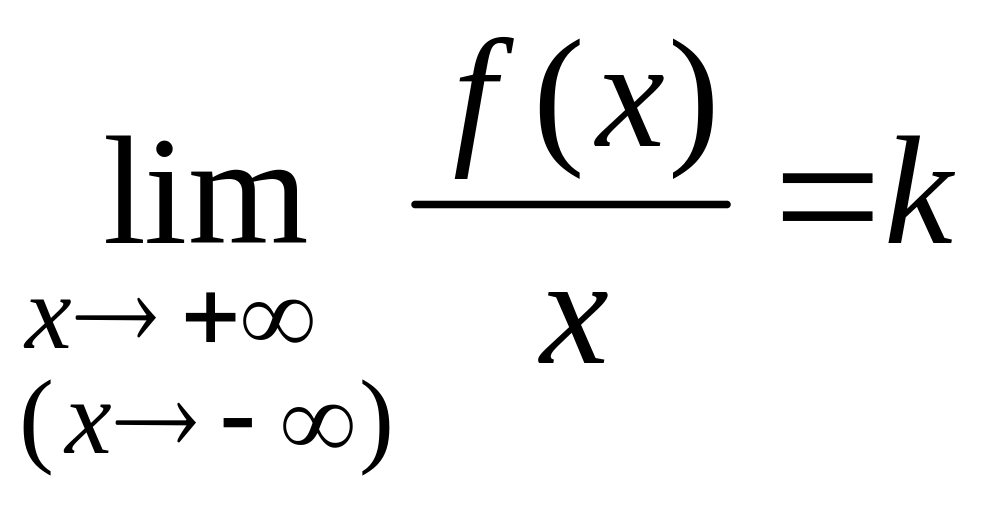, (1) . (2)

Доказательство.

1) Необходимость.

Пусть прямая y=kx+b – наклонная асимптота графика функции при х+. Тогда по определению f(x)=kx+b+(х), где . Отсюда

,

.

2) Достаточность.

Пусть существуют пределы (1) и (2). Из (2) следует f(x)-kx=b+(х), где . Следовательно, f(x)=kx+b+(х), и, значит, прямая y=kx+b является наклонной асимптотой графика функции f(x) при х+.

Пример. Найти асимптоты графика функции .

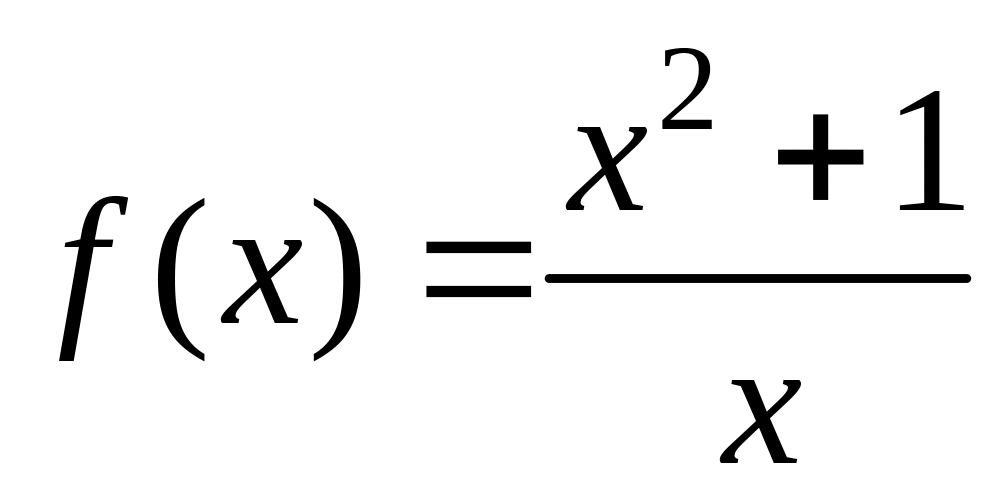 1) Вертикальные асимптоты.

.

Функция является элементарной, следовательно, непрерывна в области определения, х=0 – точка разрыва. Найдем односторонние пределы в этой точке:

, .

Следовательно, х=0 – точка разрыва второго рода, прямая х=0 – вертикальная асимптота графика функции.

2) Наклонные асимптоты.

1 способ (по определению). 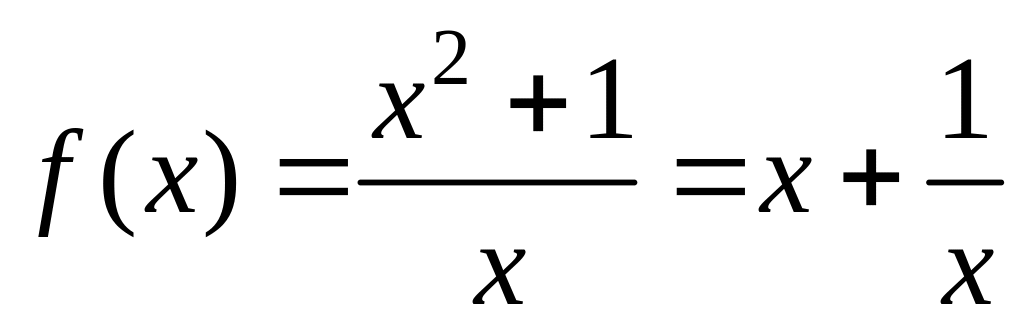. Т. е. f(x)=kx+b+(х), где k=1, b=0, . Значит, прямая y=x – наклонная асимптота графика функции при х.

2 способ (по теореме).

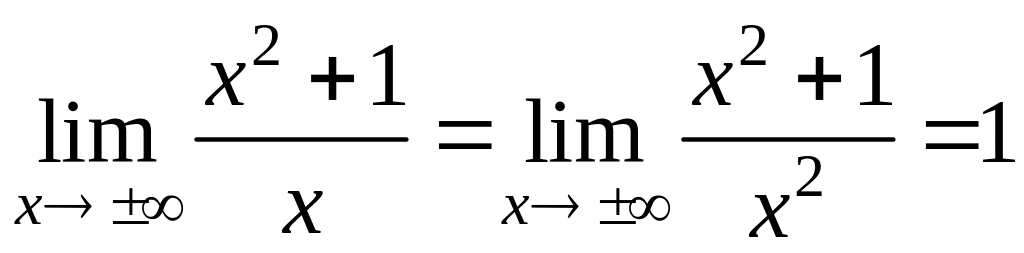 k=1,

 b=0. Следовательно, прямая y=x – наклонная асимптота графика функции при х. 

Схема полного исследования функции.

1. Найти область определения ( и множество значений, если просто).

2. Исследовать функцию на четность, нечетность, периодичность.

3. Исследовать функцию на непрерывность, найти точки разрыва и вертикальные асимптоты (если есть).

4. Исследовать поведение функции в окрестности граничных точек области определения и при х.

5. Найти (если есть) наклонные асимптоты графика функции.

6. Исследовать функцию на монотонность и экстремум.

7. Исследовать функцию на направление выпуклости и точки перегиба.

8. Найти точки пересечения графика функции с осями координат и промежутки знакопостоянства.

9. Построить график.

Пример. .

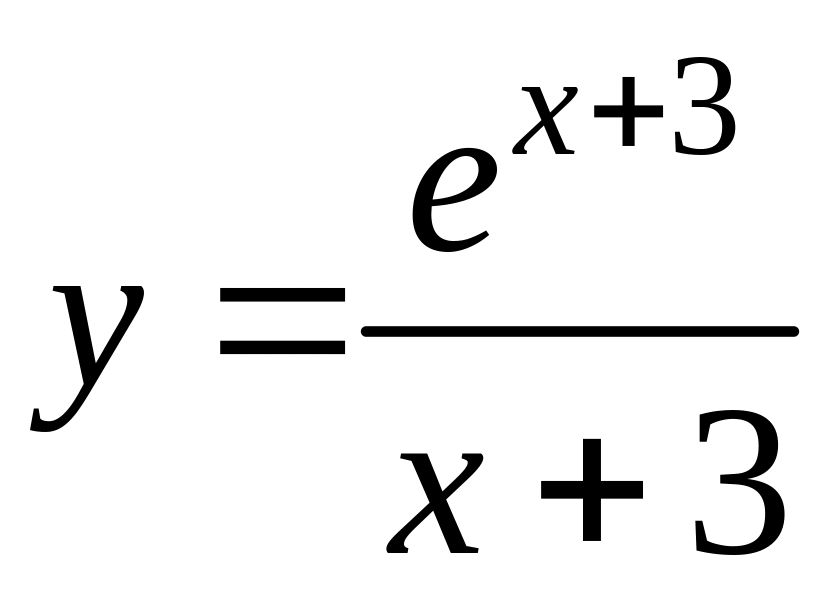1) .

2) Функция не является ни четной, ни нечетной, не является периодической.

3) х=-3 – точка разрыва.

, .

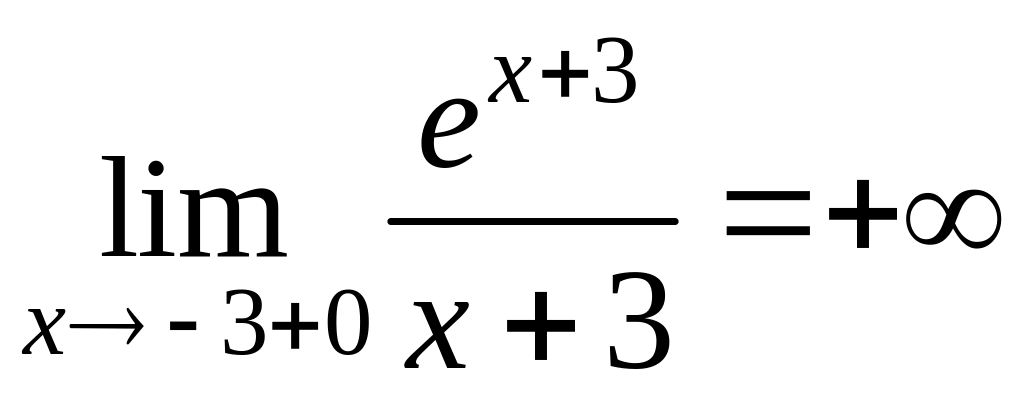Следовательно, х=-3 – точка разрыва второго рода, прямая х=-3 – вертикальная асимптота графика функции.

4) , .

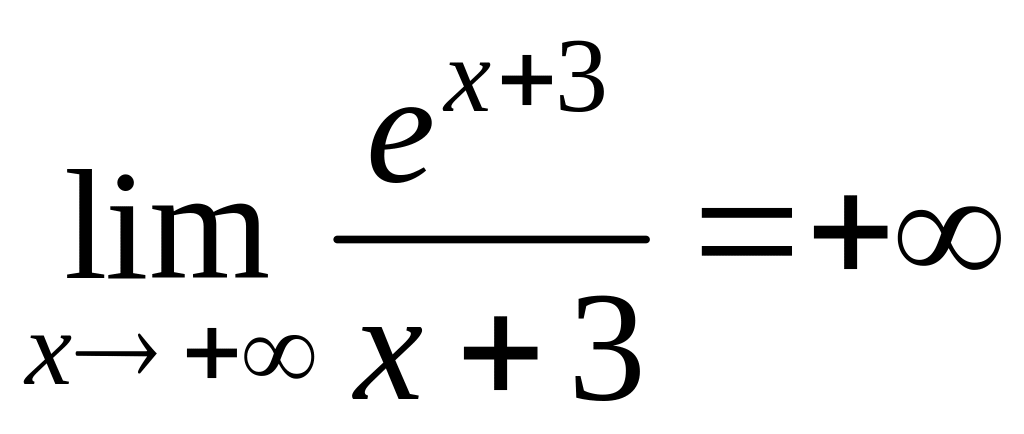5) , .

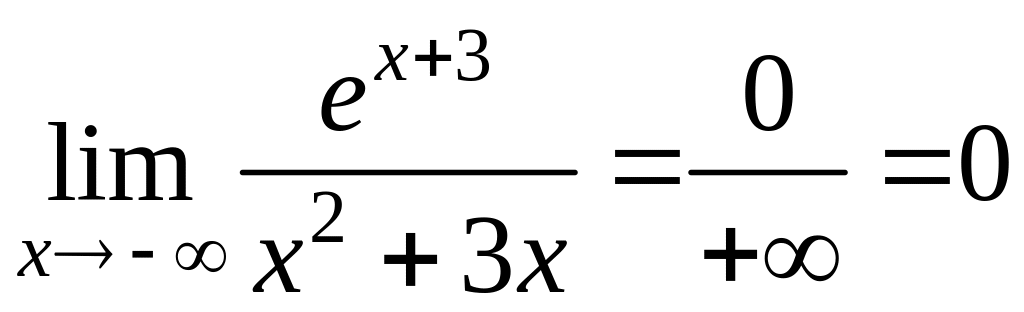При х- k=0.

.

b=0 при х-. Следовательно, прямая у=0 – горизонтальная асимптота графика функции при х-.

При х+ наклонных асимптот нет.

6 ) .

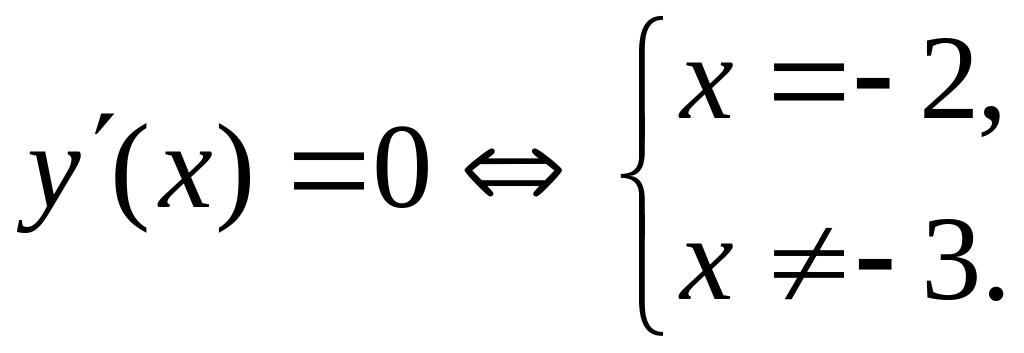
х=-2 – точка минимума, у(-2)=е – минимум.

7)

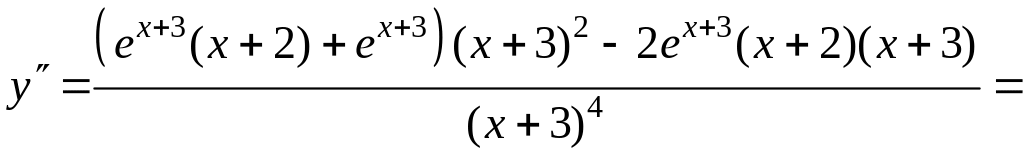
на D(f), y не существует в точке х=-3.

Точек перегиба нет.

8) Ось Ох график не пересекает.

Ось Оу: х=0, .

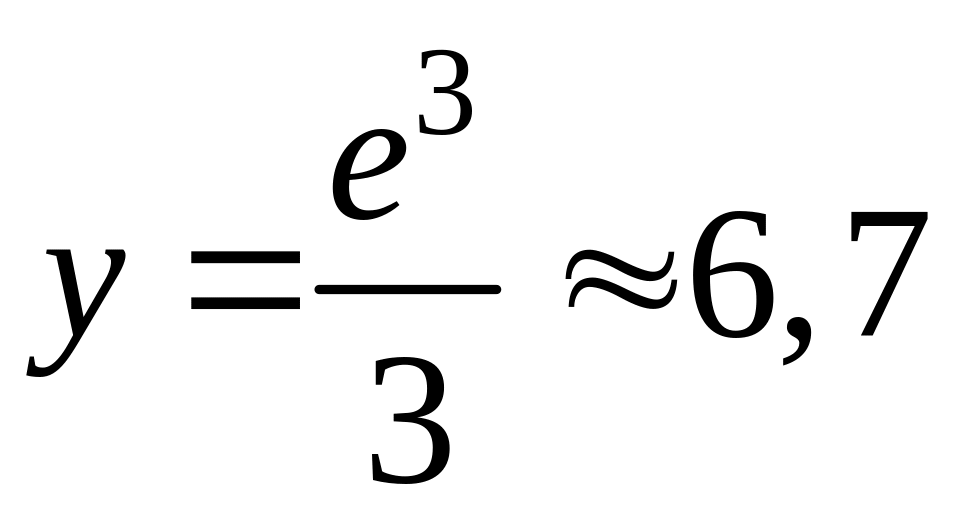y >0 при x(-3;+), y<0 при x(-;0).

47