Дифференциальное исчисление функций одной переменной

§1. Производная

Пусть функция f определена в V(x₀). Придадим точке х₀ произвольное приращение так, чтобы x₀+ x V(x₀). Тогда функция f(x) получит приращение

_.

Рассмотрим - функцию, определённую в .

Определение 1. Производной функции f в точке х₀ называется предел при отношения приращения функции к вызвавшему его приращению аргумента, если этот предел существует.

Обозначается , , , , .

Таким образом, по определению 1 . (1)

Обозначения ввёл Лейбниц (1646-1716), а , -Лагранж (1736-1813).

Производная функции в точке – число.

Пусть , , х V(x₀). Тогда (1) равносильно

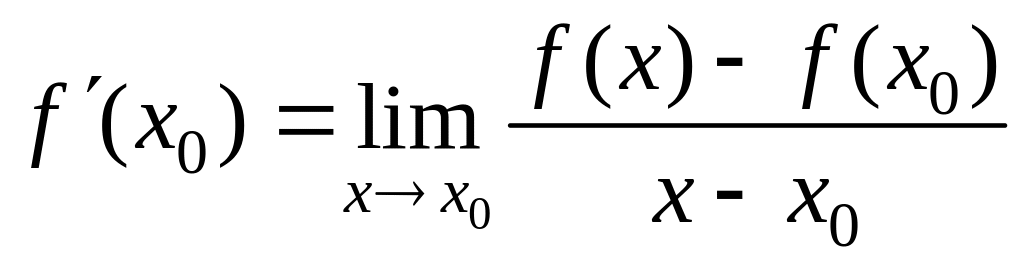. (2)

Если , то говорят, что в точке х₀ существует бесконечная производная, равная . Обозначается ( ).

Определение 2. Правой (левой) производной функции в точке х₀ называют правый (левый) предел отношения при , если этот предел существует.

, .

Правая и левая производные называются односторонними производными в точке х₀.

Справедливо следующее утверждение: функция f имеет в точке х₀ производную тогда и только тогда, когда и существуют и равны. Тогда .

Пусть f имеет производную в каждой точке . Поставим в соответствие точке х производную функции в этой точке: , . Это соответствие определяет функцию аргумента х, определённую на . Она называется производной функцией от функции f.

Значение в точке х является производной функции в точке х (может быть числом, ).

Примеры.

1) y=f(x)=c . .

 Выберем , придадим значению х приращение . Тогда

.

.

Производная постоянной функции тождественно равна нулю: .

2) y=f(x)=x, .

 Выберем , придадим значению х приращение . Тогда

. 

.

3) y=f(x)=|x| .

 Пусть х<0, .

Пусть х>0, .

Пусть х=0, ,

.

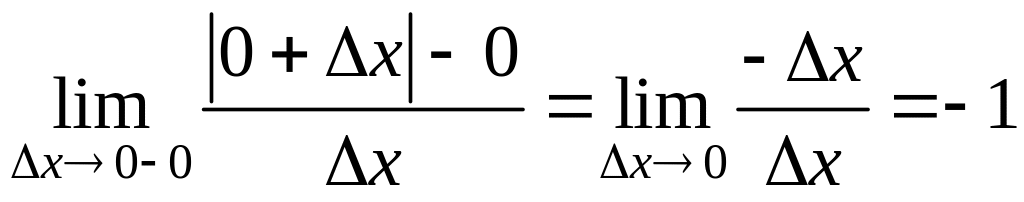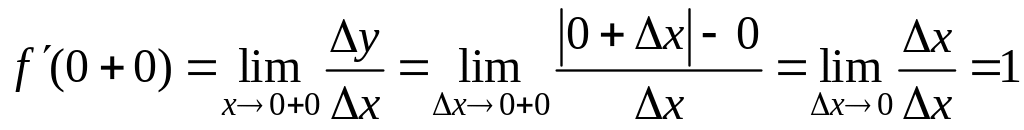Т.к. ,то не существует. 

§2. Дифференцируемость и дифференциал функции

1. Дифференцируемость функции

Пусть y=f(x) определена в некоторой окрестности точки х₀ V(х₀). Возьмём : , .

Определение 1. Функция f(x) называется дифференцируемой в точке х₀, если её приращение в этой точке, соответствующее приращению аргумента , может быть представлено в виде

, (1)

где - некоторое число, не зависящее от ,

- функция от , бесконечно малая при , т.е. .

Замечание 1. В (1) мы предполагали, что . Значит, в точке функция , вообще говоря, не определена. Будем считать, что . В таком случае непрерывна в точке , и равенство (1) справедливо и при .

Замечание 2. Так как при , то . Тогда (1) можно записать в виде:

. (2)

Пример. Доказать, что функция дифференцируема в точке х=1.

 Придадим х=1 приращение , получим . Тогда

.

Здесь А=-1, . Значит, f(x) дифференцируема в точке х=1. 

Теорема 1 (необходимое и достаточное условие дифференцируемости). Для того, чтобы функция f(x) была дифференцируема в точке х₀ необходимо и достаточно_, чтобы она в этой точке имела производную , при этом .

Доказательство.

1) Необходимость.

Пусть f(x) дифференцируема в точке х_0, т. е. , где . Пусть . Тогда .

Так как существует правой части: , то существует и левой части: , и эти пределы равны: .

2) Достаточность.

Пусть существует , то есть существует . Тогда по необходимому и достаточному условию существования предела функции в точк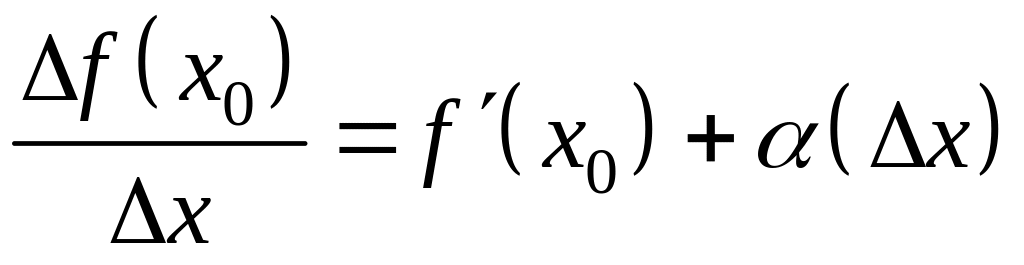е , где - бесконечно малая при . Следовательно, по определению (1) f(x) дифференцируема в точке х_0.

Из этой теоремы следует определение 2, эквивалентное определению 1.

Определение 2. Функция f(x) называется дифференцируемой в точке х₀, если она в этой точке имеет конечную производную.

Операция нахождения производной функции f(x) в точке или на множестве называется дифференцированием функции f(x).

Теорема 2 (непрерывность дифференцируемой функции). Если функция f(x) дифференцируема в точке х₀, то она непрерывна в этой точке.

Доказательство.

Так как f(x) дифференцируема в точке х₀, то

.

Значит, по определению функция непрерывна в точке х₀.

Следствие. Если функция f(x)имеет в точке х₀ производную, то она непрерывна в этой точке.

Замечание. Предположение, обратное т. 2, неверно. Функция, непрерывная в точке х₀, может не быть не дифференцируемой в этой точке.

Пример. y=f(x)=|x| - непрерывна в точке х₀=0, но не дифференцируема в ней.