
- •Содержание
- •Лабораторная работа №1 «Основы работы в Microsoft Excel» Структура рабочей книги
- •Работа с ячейками
- •Ввод чисел, даты и времени
- •Редактирование содержимого ячейки
- •Ввод формул
- •Ввод сложных функций
- •Типы ссылок
- •Автозаполнение
- •Задание
- •Лабораторная работа №2 «Логические выражения»
- •Задание
- •Лабораторная работа №3 «Диаграммы» Типы диаграмм
- •Форматирование диаграмм
- •Задание
- •Лабораторная работа №4 «Матричные вычисления» Встроенные функции работы с матрицами
- •Порядок ввода формулы
- •Задание
- •Лабораторная работа № 5 «Решение слау» Метод Кармера
- •Задание
- •Лабораторная работа №6 «Подбор параметра»
- •Задание
- •Лабораторная работа №7 «Поиск решения»
- •Лабораторная работа №8 «Функции просмотра и ссылок»
- •Задание
- •Лабораторная работа №9 «Работа с таблицами данных»
- •Сортировка
- •Фильтрация данных
- •Автофильтр
- •Фильтрация числовых данных в расширенном фильтре
- •Фильтрация текста
- •Критерии с использованием формул
- •Промежуточные итоги
- •Сводные таблицы
- •Задание
- •Литература
Задание
Найти все корни уравнения.
 .
. .
. .
.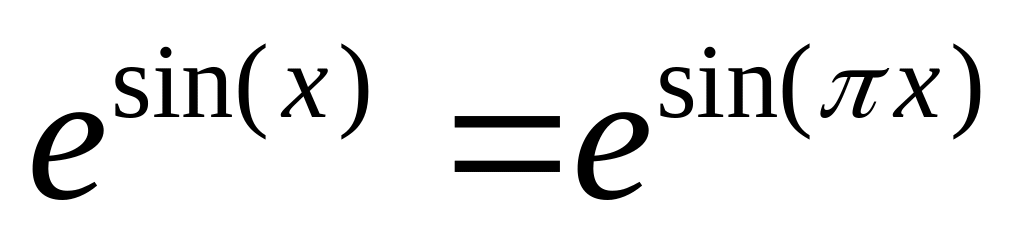 на отрезке
на отрезке
 .
. на отрезке
на отрезке
 .
. .
. на отрезке
.
на отрезке
. .
. .
. .
. .
.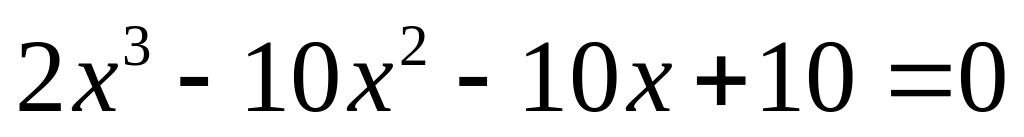 .
.
Лабораторная работа №7 «Поиск решения»
Надстройка Поиск решения предназначена для решения задач оптимизации, которая в общем виде должна состоит из:
Целевой функции
![]() .
.
Ограничений (граничных условий)
![]() ,
,
![]() ,
,
![]() .
.
Для запуска поиска решения нужно выделить целевую ячейку, в которой содержится исследуемая функция, и выбрать команду Поиск решения меню Сервис. В диалоговом окне «Поиск решения» используются следующие поля и команды:
Установить целевую ячейку — указывается адрес целевой ячейки.
Равной — служит для выбора варианта оптимизации значения целевой ячейки (максимизация, минимизация или подбор заданного числа). Число необходимо ввести в поле.
Изменяя ячейки — служит для указания ячеек, содержащих аргументы, значения которых изменяются в процессе поиска решения до тех пор, пока не будет выполнено условие оптимизации.
Ограничения — служит для отображения списка граничных условий поставленной задачи.
Добавить — используется для отображения диалогового окна «Добавить ограничение».
Изменить — применяется для отображения диалогового окна «Изменить ограничение».
Удалить — служит для снятия указанного ограничения.
Выполнить — используется для запуска поиска решения поставленной задачи.
Закрыть — служит для выхода из окна диалога без запуска поиска решения.
Пример. Предприятие выпускает 2 вида продукции - по Ct1 и Ct2 рублей за единицу. Для выпуска продукции выделено R единиц ресурсов и T нормо-часов. На выпуск единицы продукции 1-го и 2-го вида уходит по dR1 и dR2 единиц ресурсов и dT1 и dT2 нормо-часов, соответственно. Сколько нужно произвести продукции первого и второго видов, чтобы ее общая стоимость была максимальна? Данные приведены ниже.
Ct1=8.5, Ct2=9.5, R=5000, T=180, dT1=3.5, dT2=2.8, dR1=60, dR2=90.
Шаг 1. Введем исходные данные и их значения в ячейки A1:H2 (рисунок 20). Искомые значения количества произведенных видов продукции x1 и x2 введем в ячейки I1:J1, а их начальные значения в ячейки I2:J2. Присвоим ячейкам, содержащим значения параметров, имена параметров. Для этого выделим диапазон ячеек A1:J2 и выполним действие: Вставка | Имя | Создать | в строке выше.
Шаг 2. Выделим целевую ячейку B4 и вызовем действие Поиск решения. Диалоговое окно заполним, как показано на рисунке 21.
Шаг 3. Ограничениями являются следующие условия:
а) суммарные затраты ресурсов - SR и нормо-часов – ST не должны превышать выделенных значений R и T соответственно;
б) значения x1 и x2 положительные и целые.
Ограничения вводятся по команде Добавить как показано на рисунке 22.
Шаг 4. По окончании заполнения диалогового окна Поиск решения нажмем на команду Выполнить. В ячейках I2 и J2 получим искомые значения. Выберем типы отчетов «Результаты» и «Устойчивость». При этом в книгу слева от ярлычка рабочего листа добавляются ярлычки новых листов.

Рисунок 19

Рисунок 20

Рисунок 21
Задание.
Задача 1. Двум погрузчикам разной мощности не более чем за 24 часа нужно погрузить на первой площадке 230 тонн, на второй – 18 тонн. Первый погрузчик на первой площадке может погрузить 10 тонн в час, на второй – 12 тонн в час. Второй погрузчик на каждой площадке может погрузить по 13 тонн в час. Стоимость работ, связанных с погрузкой одной тонны первым погрузчиком на первой площадке, - 8 y.e., на второй – 7 y.e. Стоимость работ, связанных с погрузкой одной тонны вторым погрузчиком на первой площадке - 12 y.e., на второй – 13y.e.
Нужно составить план работы, т.е. найти, какой объем работ должен выполнить каждый погрузчик на каждой площадке, чтобы стоимость всех работ по погрузке была минимальной. Следует учесть, что по техническим причинам первый погрузчик на второй площадке должен работать не более 16 часов.
Задача 2. На производстве готовятся три типа смеси (смесь А, смесь В и смесь С) с использованием при приготовлении ингредиентов трех видов (ингредиент 1, ингредиент 2 и ингредиент 3). Расход ингредиента 1 в граммах на смеси А, В и С составляет 20, 50, 10 соответственно; ингредиента 2 — 20, 0, 40; ингредиента 3 — 20, 10, 10. Стоимость приготовления каждой смеси 100 руб. Ежедневно поступает 5 кг ингредиента 1 и по 4 кг ингредиентов видов 2 и 3. Каково оптимальное соотношение дневного производства?
Задача 3. Фабрика выпускает три вида тканей, причем суточное плановое задание составляет не менее 90 м тканей первого вида, 70 м – второго и 60 м – третьего. Суточные ресурсы следующие: 780 единиц производственного оборудования, 850 единиц сырья и 790 единиц электроэнергии, расход которых на один метр тканей представлен в таблице. Цена за 1 м ткани вида I равна 80 у.е., II – 70 у.е., III – 60 у.е. Определить, сколько метров ткани каждого вида следует выпустить, чтобы общая стоимость выпускаемой продукции была максимальной.
Ресурсы |
Ткани |
||
I |
II |
III |
|
Оборудование |
2 |
3 |
4 |
Сырье |
1 |
4 |
5 |
Электроэнергия |
3 |
4 |
2 |
Задача 4. Имеется квадратный лист жести со стороной L. По его углам вырезаются 4 одинаковых квадрата со стороной А, затем полученная крестообразная заготовка сгибается в прямоугольную коробку без верхней крышки, а швы завариваются. Какой должна быть величина А, чтобы объем получившейся коробки был максимальным? При решении принять L=1.
Задача 5. Институт заключил контракт на организацию практики с двумя предприятиями, которые могут принять, соответственно, на 300 и 200 человек. Для работы предлагается объект №1, объект №2 и объект №3. Составьте распределение студентов так, чтобы это обошлось институту возможно дешевле, если объект №1 принимает 90 человек, объект №2 — 124 человек, а объект №3—180 человек; плата института за проведение практики организациями выражается таблицей:
организация |
объект №1 |
объект №2 |
объект №3 |
1 |
200 |
300 |
150 |
2 |
400 |
700 |
150 |
Задача 6. Для питания нужно ежедневно принимать не менее 6 единиц белков, 8 единиц жиров и 12 единиц углеводов. Есть два вида корма. Одна единица первого корма содержит 21 единицу белка, 2 единицы жира, 4 единицы углеводов и стоит 3 руб, Для второго корма соответствующие цифры cледующие: 3, 2, 2 и 2. Составьте оптимальный рацион питания.
Задача 7. Продукцию, производимую на предприятиях А и В, надо развезти но строительным площадкам № 1, № 2 и № 3. Предприятие А производит 320 единиц продукции, предприятие В — 380. Строительная площадка № 1 реализует за сутки 200 единиц продукции, № 2 — 280 ед., № 3 — 220 ед.. Составьте план перевозок продукции, при котором их стоимость будет наименьшей, если стоимость перевозки 1 единицы продукции из предприятия А на площадки № 1, № 2 и № 3 равна 2, 4, 6, соответственно; из предприятия В — 2, 5, 3.
Задача 8. Производственная мастерская планирует выпуск двух видов изделий: изделие1 и изделие2. На изделие1требуется 1 м шерсти, 2 м лавсана и 1 человеко-день трудозатрат. На изделие2— 3,5 м шерсти, 0,5 м лавсана и 1 человеко-день трудозатрат. Всего имеется 350 м шерсти и 240 м лавсана, 150 человеко-дней трудозатрат. Предусматривается выпуск не менее 110 изделий, причем необходимо обеспечить прибыль не менее 1400 руб. Определите оптимальное количество изделий каждого вида, если прибыль от реализации изделия1 составляет 10 руб., а изделие2 — 20 руб.
Задача 9. Составьте план производства двух видов продукции, чтобы стоимость произведенного была максимальной, если: цена 1 единицы каждой продукции по 20 денежных единиц. На каждую единицу первой продукции расходуется 2 единицы сырья; 4 единицы материалов и 1 человеко-день; второй продукции — соответственно, 2, 3 и 3. Общие объемы ресурсов: фонд рабочего времени — 12; фонд сырья — 16; фонд материалов — 9; цена 1 единицы сырья —1 денежная единица; цена материалов — 3 денежных единицы.
Задача 10. Цех малого предприятия должен изготовить 100 изделий трех типов и не менее 20 штук изделий каждого типа. На изделия уходит 4, 3.4 и 2 кг металла соответственно, при его общем запасе 340 кг, а также расходуются по 4.75, 11 и 2 кг пластмассы, при ее общем запасе 400 кг. Прибыль, полученная от каждого изделия равна 4, 3 и 2 р. Определить сколько изделий каждого типа необходимо выпустить для получения максимальной прибыли в рамках установленных запасов металла и пластмассы.
Задача 12. В качестве тестового функционала при поиске точки минимума часто используется функционал Розенброка:
![]() .
.
«Поверхность» этого функционала
напоминает глубокий овраг, что сильно
осложняет работу многих алгоритмов
минимизации. Требуется вычислить точку
минимума функционала при ограничениях:
![]() .
.
Задача 13. Для производства 2-х видов товара выделено ресурсов: трудовых — 48, сырьевых — 56, материалов — 72. Затраты на производство первого товара составляет трудовых — 6, сырьевых — 8, материалов — 6, а затраты на производство второго товара составляют — 5, 7, 5, соответственно. Сколько нужно произвести товара первого и второго вида, чтобы стоимость всей продукции была максимальной, если: цена одной единицы сырья — 2 денежные единицы; материалов — 1,5 денежные единицы.
Задача 14.
Дан функционал: F(a,b)
= 100(a – b)2
– 50a/b и
ограничения в виде:
![]()
Определить значения a, b, доставляющие максимальное значение функционала и удовлетворяющие неравенствам.
