1.5.5.Теоремы разложения

В теории логических функций особо важное значение имеет теорема разложения Шеннона: любую функцию F(v) можно разложить по переменной x_p в форме:

По принципу двойственности получается двойственная теорема разложения:

С теоремой разложения связаны тождества

1.6.Представление логической функции в виде сднф и скнф

Логическая функция дизъюнктивной формы (ДФ): - представляет собой дизъюнкции отдельных членов, каждой из которых, в свою очередь, есть некоторая функция, содержащая только конъюнкции и инверсии.

- где f функция 3х переменных.

Логическая функция дизъюнктивной нормальной формы (ДНФ): - форма представления дизъюнктивной функции, в которой инверсия применяется лишь непосредственно к аргументам (переменным), но не к более сложным функциям от этих аргументов.

- где f функция 3х переменных.

Логическая функция совершенной дизъюнктивной нормальной формы (СДНФ): - если каждый член дизъюнктивной нормальной функции от n аргументов содержит все эти n аргументы, часть из которых входит в него с инверсией, а часть без нее.

- где f функция 3х переменных.

Логическая функция конъюнктивной формы (КФ): - представляет собой конъюнкцию отдельных членов, каждой из которых, в свою очередь, есть некоторая функция, содержащая только дизъюнкции и инверсии.

- где f функция 3х переменных.

Логическая функция конъюнктивной нормальной формы (КНФ): - форма представления конъюнктивной функции, в которой инверсия применяется лишь непосредственно к аргументам (переменным), но не к более сложным функциям от этих аргументов.

- где f функция 3х переменных.

Логическая функция совершенной конъюнктивной нормальной формы (СКНФ): - если каждый член конъюнктивной нормальной функции от n аргументов содержит все эти n аргументы, часть из которых входит в него с инверсией, а часть без нее.

- где f функция 3х переменных.

1.6.1.Первичные термы

Терм: - это переменные, инверсии переменных, их конъюнкция и дизъюнкция.

Первичные термы: - переменные и их инверсии.

Для первичных термов будем использовать обозначение - где e_p = 0 или 1. В общем случае - подставляем сюда значения e_p = 0 или 1 получим:

• при e_p = 0 то

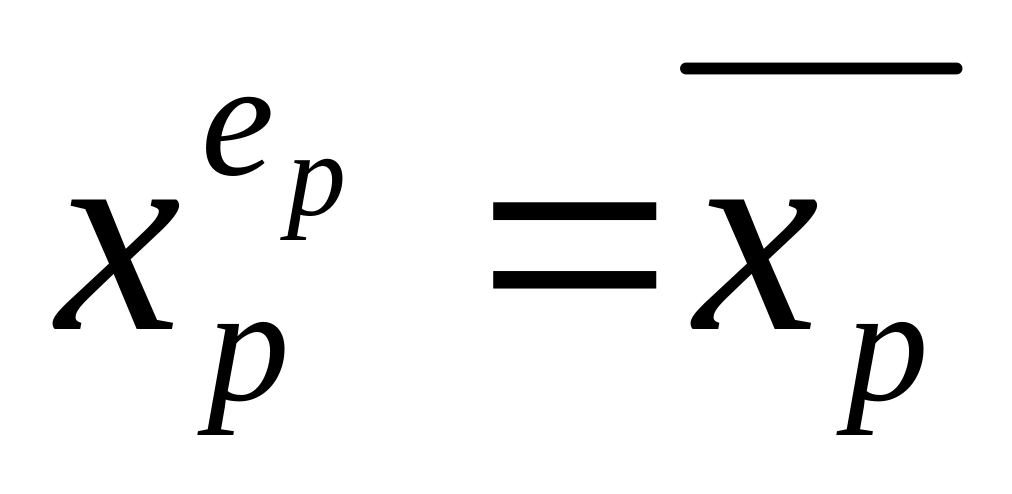
• при e_p = 1 то

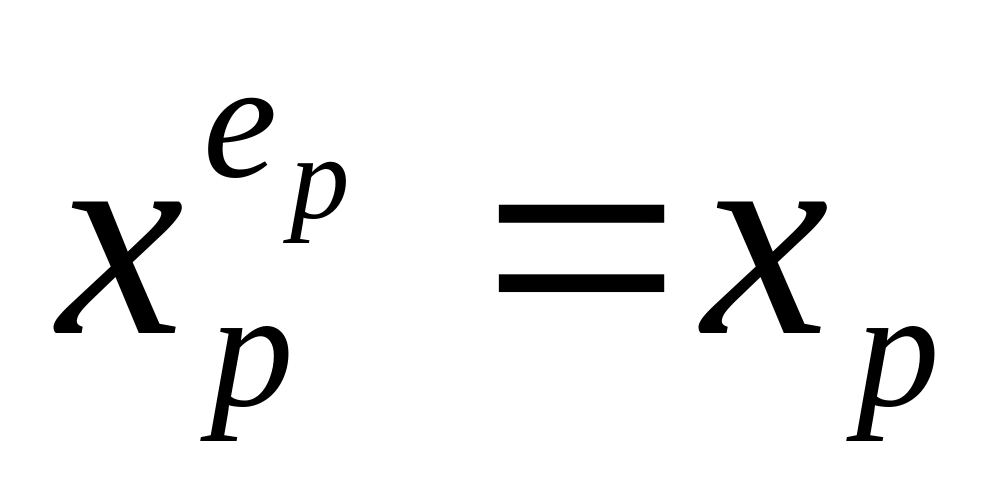
Такое обозначение облегчает формализацию общих соотношений для логических функций:

• 

• 

• 

1.6.2.Минтермы и макстермы

Минтерм: - конъюнкция всех переменных, которые входят в прямом виде, если значение данной переменной в точке определения равно 1, либо в инверсном виде, если значение переменной равно 0.

Обозначение термов позволяет в общем виде записать конъюнкцию любого числа аргументов.

Минимальным термом – минтермом: - называется функция n переменных:

Vi	x1,x0
0	0 0
1	0 1
2	1 0
3	1 1

где v=(x_n-1,…,x₀), e_p = 0 или 1

Из данного определения следует, что имеется 2ⁿ – различных минтермов n переменных т.к. минтерм представляет n разрядное двоичное число от 0 до 2ⁿ –1.

Запишем все минтермы двух переменных

Макстерм: - это дизъюнкция всех переменных, которые входят в прямом виде, если значение данной переменной в точке области определения равно 0, либо в инверсном виде, если значение переменной равно 1.

Vi	x1,x0
0	0 0
1	0 1
2	1 0
3	1 1

Максимальным термом – макстермом: - называется функция n переменных

где v=(x_n-1,…,x₀), e_p = 0 или 1

Запишем все макстермы двух переменных