1.4.Алгебра логика

В алгебре логики рассматриваются следующие компоненты:

• переменные, могут принимать только два значения 0 и 1, переменные будем обозначать латинскими буквами x,y,z…, а также x₀,x₁,…x_n, y₀,y₁,…y_n и т.д.;

• отношение эквивалентности (равенства «=»), удовлетворяет следующим свойствам:

• рефлексивность – x=x;

• симметричность – если x=y то y=x;

• транзитивность – если x=y и y=z то x=z, отсюда следует принцип, если x=y, то в любой формуле, содержащей x, в место x можно подставить y, и в результате будет получена эквивалентная формула;

• три операции:

• дизъюнкция, операция ИЛИ, логическое сложение. Обозначают знаком ∨ или +;

• конъюнкция, опе6рация И, логическое умножение, обозначается знаком ∧, или &, или *, или опускается;

• отрицание, инверсия, операция НЕ, обозначается чертой над переменной, или над элементами 0 и 1, или над операциями с охватом всех переменных входящих в операцию ( );

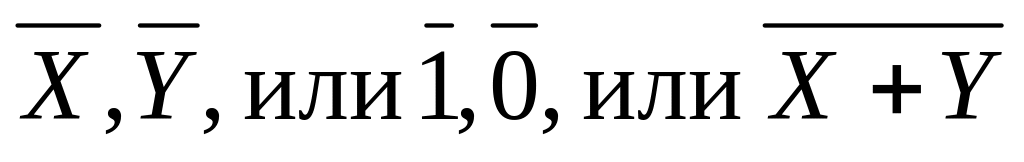1.4.1.Аксиомы алгебры логики

Формула (1.1) – утверждает, что в алгебре логики рассматриваются только двоичные переменные.

Формулы (1.2)-(1.4) – определяют операции дизъюнкции и конъюнкции.

Формула (1.5) – определяет операцию отрицания.

1.4.2.Теоремы и тождества алгебры логики

На основании аксиом алгебры логики можно вывести ряд теорем и законов.

1. Идемпотентные законы (1.6)

2. Коммутативные законы 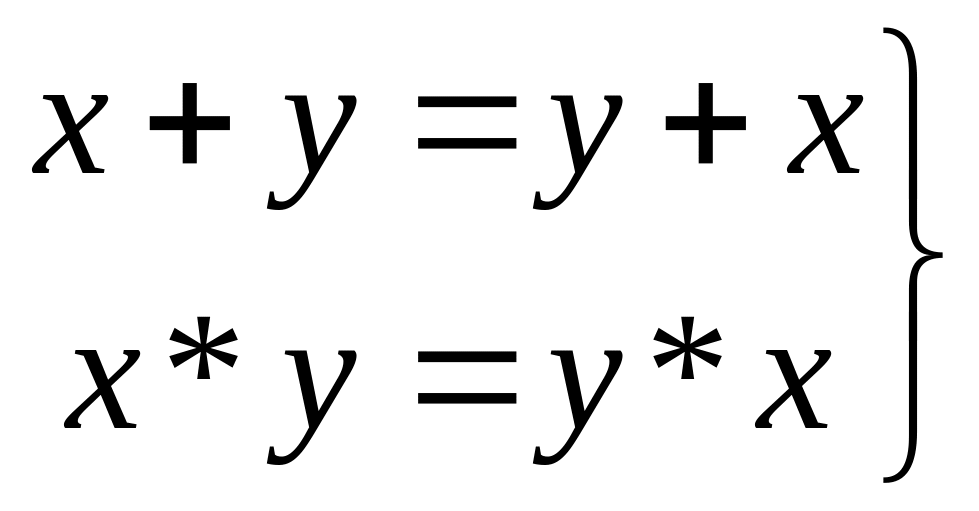(1.7)

3. Ассоциативные законы 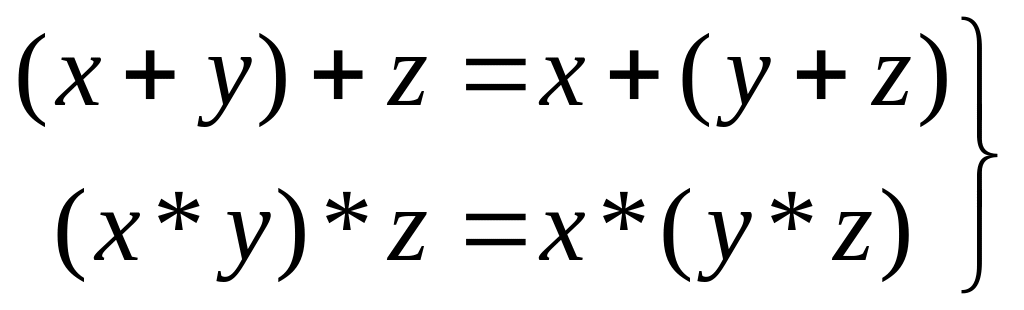(1.8)

4. дистрибутивные законы 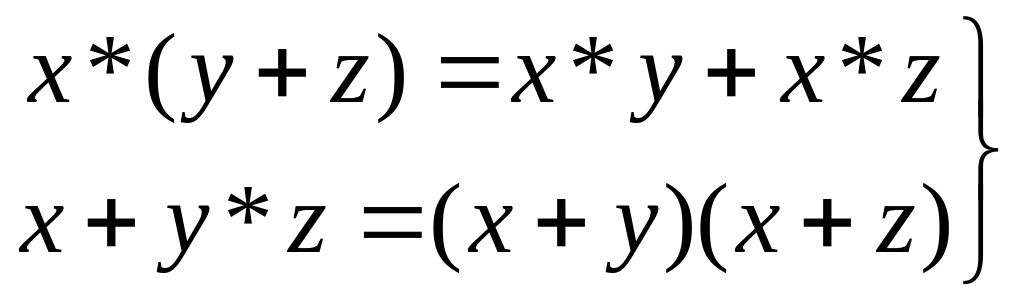(1.9)

5. Законы отрицания 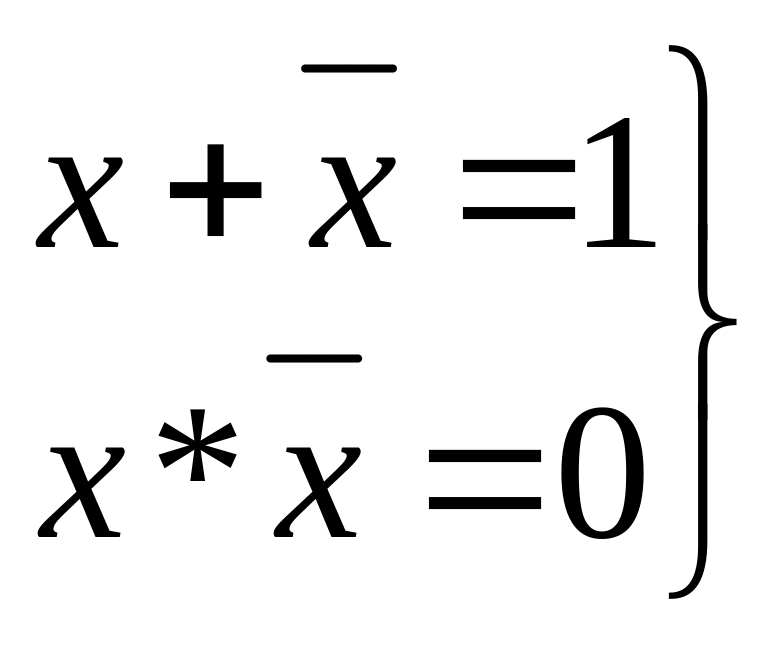(1.10)

(1.11)

(1.12)

6. Законы двойственности (теоремы де Моргана)

(1.13)

7. Закон двойного отрицания 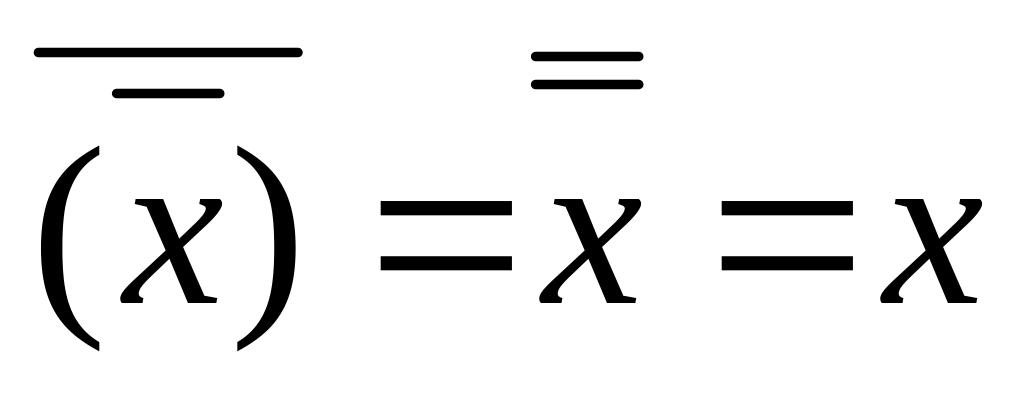(1.14)

8. Законы поглощения (1.15)

9. Операции склеивания 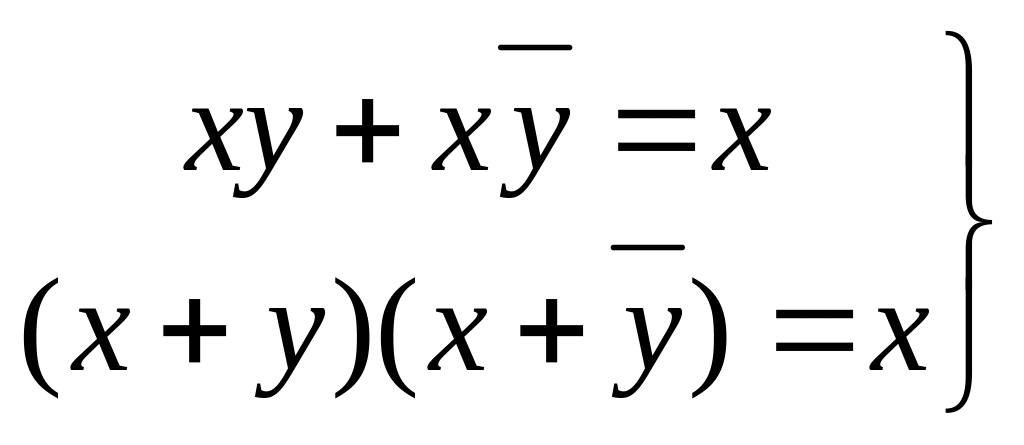(1.16)

(1.17)

Большинство теорем, а также аксиом записаны парами. При внимательном изучении пар можно вывести принцип двойственности – если в тождестве произвести взаимные замены операций дизъюнкции и конъюнкции, а также элементы 0 и 1, если они имеются то получим тоже тождество. Такое свойство называется принципом двойственности.

f(v,0,l/+,&)=g(v,0,/+,&) где v=(x_n-1,...,x₀) то справедливо также тождество: f(v,l,0/&,+)=g(v,l,0/&,+)

Все теоремы могут быть доказаны аналитически или методом перебора.

1. Метод перебора – тождество (1.13)

XY
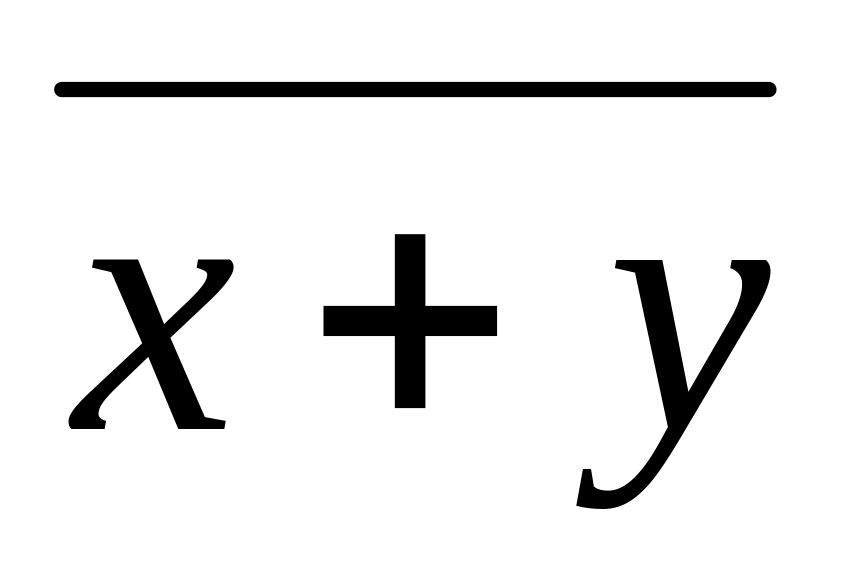
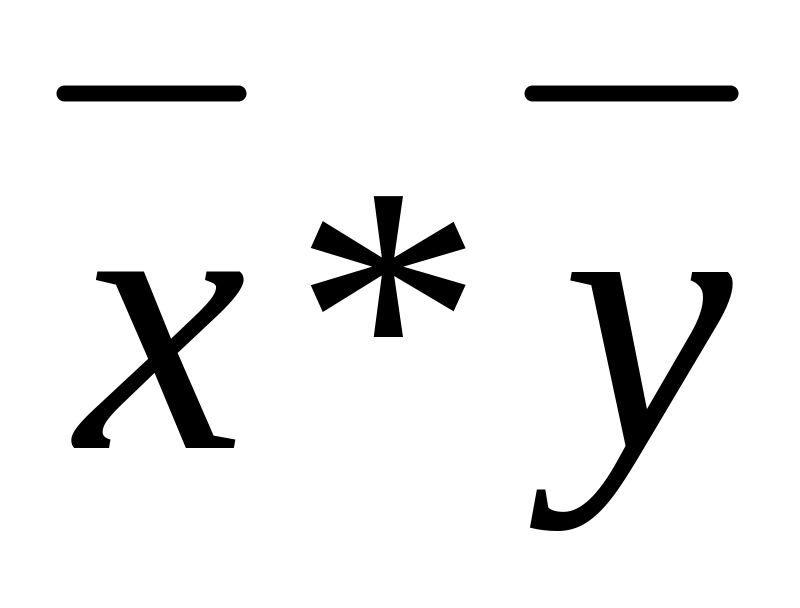
0 0
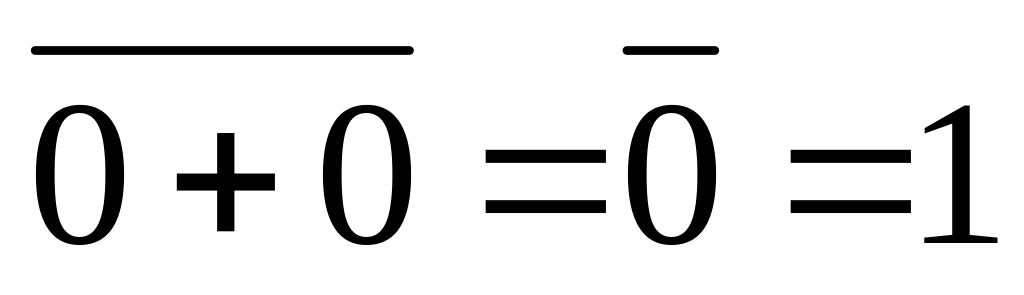
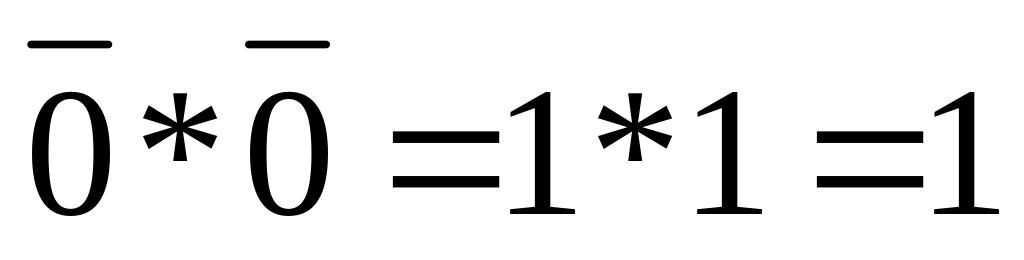
0 1
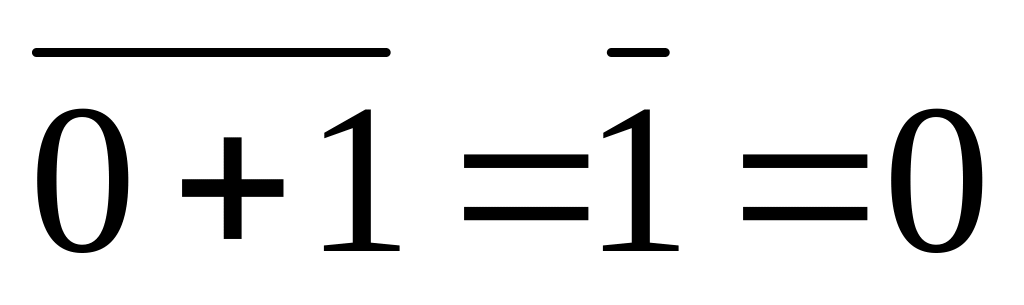
1 0
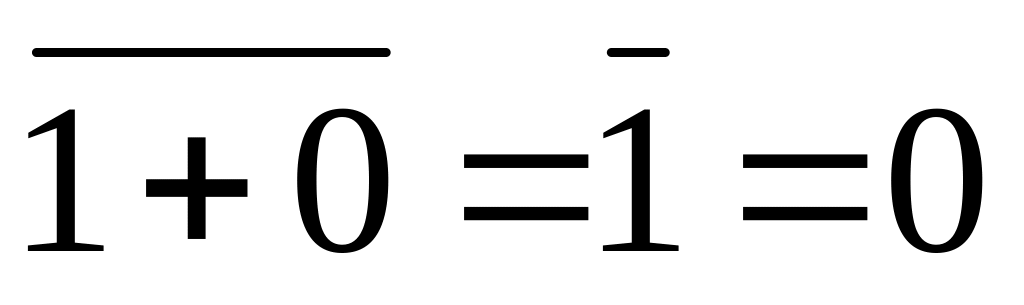
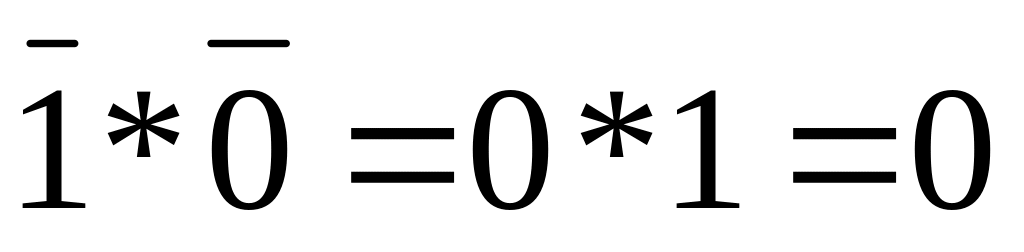
1 1

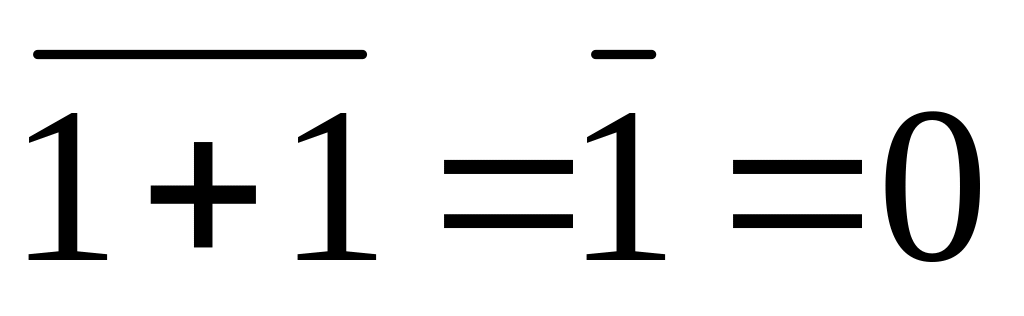
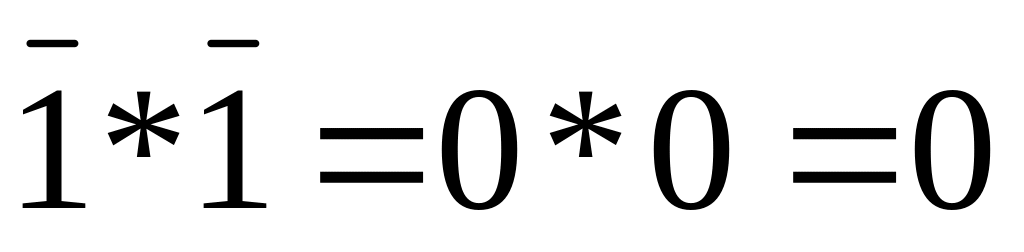
2. Аналитический метод – тождество (1.17)

Порядок выполнения операций:

• отрицание слагаемой или сомножителя;

• конъюнкция сомножителей;

• дизъюнкция слагаемых;

• общее отрицание дизъюнкции или конъюнкции.

1.5.Логические функции

Логическая функция – это логическое выражение, состоящее из логических переменных связанных между собой с помощью операций алгебры логики.

В соответствии с выше приведенными аксиомами (1.1)-(1.5) функция может принимать в зависимости от значений переменных x_p только два значения 0 и 1.

Для функции n переменных x_n-1,…,x₀ будем использовать общее обозначение где v=(x_n-1,…,x₀) каждая переменная x_p (p=0,1,2,…,n) может принимать только два значения 0 и 1. Поэтому число всех возможных комбинаций значений x_n-1,…,x₀ конечно и равно 2ⁿ.

В общем виде конкретное значение переменной x_p (0 или 1) будем обозначать через e_p. Символами i, j и т.п. будем обозначать порядковые десятичные числа. e_n-1…e_p…e₀ – обобщающая запись двоичного числа, где e_p = 0 или 1, и являются элементами алгебры логики если они используются в качестве значений переменных, для этих элементов не существует соотношений больше или меньше.