9. Случайные сигналы. Общие сведения

Сигналы – это физические процессы, т.е., явления, совершающиеся во времени. К случайным относят сигналы, поведение которых во времени не известно. Именно такие сигналы являются носителями информации.

Случайный сигнал при чередовании сеансов передачи – приема, которые можно назвать опытами, проявляет себя не одинаково. Его отдельное проявление в одном сеансе передачи - приема называют реализацией или траекторией. Сам же случайный сигнал состоит, в общем, из бесконечного множества реализаций, в целом не совпадающих одна с другой, но имеющих общие точки их (рис.1).

а) б)

Рис.1. Непрерывный (а) и дискретный (б) случайные сигналы

Случайные сигналы для простоты будем обозначать теми же символами, что и детерминированные. Например, - непрерывный и , - дискретный (цифровой) случайные сигналы; - число отсчетов (значений) дискретного сигнала. При отражении случайного сигнала, как совокупности реализаций, реализации будем обозначать теми же символами, что и сигнал, с указанием в индексе номера реализации. Например, - реализация непрерывного, а , , - дискретного случайного сигнала; здесь 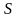- число реализаций, оно может быть бесконечным в общем или конечным – в частном случае, например, в некоторой выборке при обработке сигналов в системах ЦОС.

10. Характеристики случайных сигналов

Анализ случайных сигналов осуществляется на основе теории вероятностей и теории случайных процессов. Основными характеристиками случайных сигналов являются функция математического ожидания, функции дисперсии и среднеквадратического отклонения, автокорреляционная и автоковариационная функции, а также спектр случайного сигнала.

Для определения и нахождения указанных выше характеристик построим график, моделирующий случайный сигнал

а) б)

Рис.2. Сечения случайного сигнала (а), дискретная реализация случайного сигнала (б)

Проведем через равные промежутки времени вертикальные линии, называемые сечениям. Тем самым мы рассекаем реализации случайного сигнала в одни и те же моменты времени, и тем самым мы выполняем дискретизацию случайного сигнала и его реализаций. Одна из дискретных (дискретизированных) реализаций с номером показана на рис. 2б. Ее отсчеты обозначены двойными индексами: ; первый индекс – номер отсчета в реализации, второй – номер реализации. Подобным образом обозначаются и другие реализации.

Рассмотрим некоторое -е сечение случайного сигнала (рис.3). Совокупность точек реализаций сигнала, лежащих на вертикальной линии сечения, образуют некоторое множество. Если каждой точке присвоить численное значение, равное ординате этой точки, то получим совокупность числовых значений, составляющих в целом непрерывную случайную величину. Непрерывность обусловлена тем, что в любой точке сечения может оказаться точка какой либо реализации из бесконечного множества. Таким образом, точки, принадлежащие реализациям в одном сечении, образуют непрерывную сплошную область.

Случайные величины характеризуются параметрами математического ожидания, дисперсии и среднеквадратического отклонения.

Рис.3. Сечение случайного сигнала в -й момент времени

Следует отличать математическое ожидание, дисперсию и среднеквадратическое отклонение, как параметры случайной величины, от функций математического ожидания, дисперсии и среднеквадратического отклонения, как характеристик случайного сигнала. Первые являются неслучайными величинами, вторые – неслучайными функциями.

Случайные величины в сечениях распределены по тому или иному закону (рис.4а). Закон распределения характеризует плотность вероятности попадания случайной величины в определенный диапазон (рис.4б); на рисунке заштрихованная площадка численно равна вероятности попадания значений случайной величины на отрезок (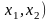 . Здесь под величиной следует подразумевать множество точек, образуемых реализациями сигнала в одном сечении; индекс-номер сечения для простоты опущен.

При известном законе распределения вероятностей математическое ожидание случайной величины равно

, (2)

а дисперсия

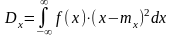. (3)

Среднеквадратическое отклонение зависит от дисперсии и определяется по формуле

.

Оценку дисперсии можно рассчитать по следующим формулам: