Специальные сигналы и спектры
Синусоидальный сигнал аналитически
представляется
синусоидальной
функцией, которая является периодической:
,
где
- амплитуда,
- угловая частота.
И амплитуда, и угловая частота – величины постоянные. Считается, что синусоидальный сигнал (рис.1, верхний) действует бесконечно долго.
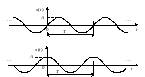Рис.
1. Синусоидальный и косинусоидальный
сигналы
Спектр такого сигнала можно найти с помощью формул для коэффициентов комплексного ряда Фурье:
.
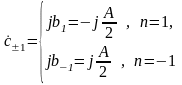(2).
Спектр
содержит только мнимую часть, состоящую
из коэффициентов
и
,
что отражается на графике спектра в
виде двух линий: одна в положительной
области частот, вторая – в отрицательной
при значениях частоты, равных
(рис. 2а). Это сравнительно легко
объясняется тем, что в сигнале
содержится только одна гармоника виде
синусоиды. Мнимый характер спектра
объясняется тем, что указанная синусоида
является нечетной функцией. При задании
сигнала в виде косинусоиды (четной
функции)
(рис.1, нижний) спектр содержал бы только
действительную составляющую (рис.2б):
.
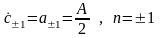а) б) Рис. 2. Спектры синусоидального и косинусоидального сигналов
На практике часто интересуются модулем спектра, т.е., абсолютными значениями составляющих спектра, В этом случае спектры синусоидальных и косинусоидальных сигналов совпадают и имеют форму, показанную на рис.2б.
Синусоидальные (косинусоидальные) сигналы используются в качестве несущих в системах амплитудной модуляции, при настройке различного рода аппаратуры для передачи, приема и обработки сигналов и т.п.
Прямоугольный импульс может задаваться в виде периодического сигнала или одиночного непериодического сигнала. И тот и другой часто приводят в качестве примеров в задачах из-за их сравнительной простоты. Кроме того, прямоугольный импульс используют как типовой сигнал при настройке и испытании разного рода аппаратуры и систем.
Аналитически прямоугольный импульс длительностью , периодически повторяющийся, задается следующей формулой для каждого периода (рис.3):
,
(3)
которая устанавливает, что значения сигнала равны постоянной в пределах времени действия импульса и равны нулю за пределами действия импульса; кроме того, сигнал расположен симметрично относительно начала координат, что свидетельствует о том, что он является четной функцией. Приведенная формула справедлива для каждого периода в отдельности в пределах .
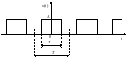Рис.3
Для периодического сигнала коэффициенты ряда Фурье вычисляются по формулам:
,
.
(4)
Сигналы
в виде четных функций не имеют
синусоидальных составляющих, свидетельством
чего является
.
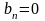На
рис. 4 приведены графики спектров для
соотношений длительности сигнала к
периоду, равных
.
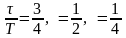Из графиков видно, что при постоянной
длительности сигнала и при увеличении
периода сигнала линии спектра сгущаются,
амплитуды гармоник уменьшаются, а форма
огибающей спектра остается неизменной.
Надо полагать, что при увеличении
периода до бесконечности спектр станет
сплошным.
Рис.4
Рассмотренные спектры занимают положительную область частот. При вычислении комплексного спектра прямоугольного импульса по формуле (5)
получают двусторонний симметричный относительно оси ординат спектр, занимающий как положительную, так и отрицательную область частот (рис.5). Форма огибающей спектра для положительной области будет такой же, как и для спектра, определенного ранее. Симметричные относительно оси ординат сигналы имеют действительные спектры, независимо оттого, по каким формулам они определялись
Непериодический прямоугольный импульс задается формулой (1) без всяких оговорок. На графике он задается одиночным импульсом (рис.6). Спектр непериодического сигнала, а, вернее, его спектральную плотность можно получить рассмотренным ранее образом, воспользовавшись формулой интегрального преобразования Фурье. После интегрирования
.
(6)
На рис.7 показан график спектральной плотности, полученной в соответствии с (6). Из сравнения графиков на рис.5 и рис.7 можно убедиться, что огибающие спектров периодического и непериодического сигналов имеют одинаковые формы. Спектр периодического прямоугольного импульса дискретный, спектр непериодического сигнала – сплошной. Тот и другой спектры действительные, так как тот и другой сигналы симметричны относительно оси ординат. Фазовый спектр таких сигналов на всех частотах равен нулю. Следует отметить, что в общем при применении комплексного ряда Фурье и интегрального преобразования Фурье, спектры, получаемые при этом, будут комплексными, если сигналы, порождающие эти спектры, не симметричны относительно оси ординат. В этом случае имеют место так же и фазовые спектры.
Синусоидальный сигнал, ограниченный во времени можно получить как произведение одиночного прямоугольного импульса на синусоидальный сигнал, бесконечно продолжающийся во времени. Зададим первый сигнал функцией
,а второй – функцией
;
результирующий сигнал будет
равен (рис.8а):
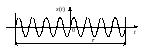а)
б)
Рис.8
.
(7)
Спектр такого сигнала можно найти, применив формулу интегрального преобразования Фурье:
.
В
последней формуле осуществлена замена
.
После интегрирования и преобразований
получим
.
(8)
Спектр содержит только мнимую составляющую, так как функция - нечетная. График ее спектра показан на рис.9а.
а)
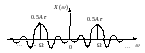б)
Рис.9
Для
ограниченной косинусоидальной функции,
полученной умножением функции
на прямоугольный импульс (рис.8б):
являющейся четной функцией
спектр определяется действительной
функцией
.
(10)График такой функции
показан на рис.9б.