1. Сигналы и их характеристики

Сигналами называют физические процессы, несущие информацию о себе или других процессах. В принципе любой процесс, вызывающий возмущения в окружающей среде, может являться сигналом, если эти возмущения воспринимаются и анализируются. Восприниматься и анализироваться сигналы могут органами чувств живых существ или техническими устройствами. Сигналы, как процессы, описываются функциями времени; однако имеют место и пространственные сигналы, например, изображения на поверхности, и пространственно-временные сигналы, например, волны в сплошной среде.

Сигналами могут являться, например, следующие процессы: изменение звукового давления в атмосфере, в воде или другой сплошной среде, измеренное во времени; колебания поверхности Земли при землетрясениях и взрывах; изменение электрического напряжения или силы тока в электрической цепи во времени; изменение освещенности участков бумаги с каким-либо изображением в зависимости от положения указанных участков; электромагнитные колебания самой различной природы, излучения далеких звезд т.п.

Сигналы обладают физическими свойствами, которые определяют их технические характеристики и параметры.

Обычно технические характеристики задаются в виде некоторых функций, описывающих сигнал, при этом функции могут представляться математическими выражениями, графиками, таблицами, словесно и т.п.

Численные значения характеристик сигнала, иначе величины этих характеристик будем называть параметрами сигнала. Другими словами, технические характеристики сигналов – это функции, описывающие свойства сигнала, а параметры – численные значения этих свойств. Зачастую на практике не делают различий между сигналом и его описанием виде функции или иным описанием.

В технической литературе сигнал обозначают как временную функцию, например, 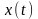, или 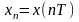, 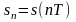и т.п. Здесь 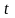- непрерывное время, 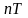- дискретное время, 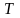- временной отрезок, называемый интервалом дискретизации; обычно - постоянно. Применяются и другие обозначения сигналов. На рис.1 показаны в общем виде графики непрерывных сигналов и дискретных .

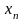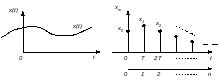
а) б)

Рис.1. Графики непрерывного и дискретного сигналов

Важнейшими характеристиками сигналов являются:

• его описание в виде временной функции;

• мощность

- его спектр или спектральная плотность, представляющие зависимость амплитуд гармонических составляющих сигнала от их частоты;

• энергетический спектр сигнала, характеризующий распределение мощности (или энергии) сигнала по частоте;

• автокорреляционная функция (автокорреляция) сигнала и взаимная корреляционная функция (взаимная корреляция) двух сигналов; та и другая выражают внутреннюю статистическую связь между отдельными значениями сигнала (автокорреляция) или внешнюю статистическую связь между отдельными сигналами (взаимная корреляция);

Сигналы могут быть естественными и искусственными (техническими). Первые имеют природное происхождение, вторые создаются в технических устройствах. Естественные сигналы, принятые техническими устройствами и преобразованные ими, следует также относить к искусственным. Естественные сигналы – это сложные процессы, одновременно охватывающие явления различного характера.

По возможности определения поведения сигналов их разделяют на детерминированные и случайные (стохастические). Детерминированные – это такие сигналы, о которых известно все. Считается, что такие сигналы информации не несут, так как их поведение можно предсказать. Тем не менее детерминированными сигналами широко пользуются при моделировании различных процессов, при настройке аппаратуры.

Носителями информации являются случайные сигналы. Случайный сигнал – это сигнал, значения параметров которого не известны, и их нельзя определить ни в ближайший, ни в любой другой момент. Считается, что случайный сигнал до его получения (восприятия), имеет полную неопределенность о себе.

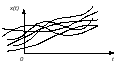
Рис. 2. Случайный сигнал, как набор реализаций

Сигналы разделяются на периодические и непериодические (апериодические). Первые повторяются через равные интервалы времени , называемые периодом, вторые таким свойством не обладают. Указанное свойство периодических сигналов можно записать аналитическ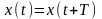и: или 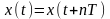для любых моментов времени; здесь 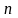- целое. Если сигнал известен в течение какого-либо периода, то, следовательно, он известен и в любой другой период. Поэтому периодические сигналы и относят к детерминированным. Не следует смешивать периоды с интервалами дискретизации, о которых говорилось ранее, так как те и другие часто обозначаются одинаково.

Для непериодических сигналов можно записать: 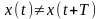или . Непериодический сигнал может быть как детерминированным, так и случайным. Периодический непрерывный сигнал показан на рис. 3, непериодический – на рис. 1. Периодическими могут быть как непрерывные, так и дискретные сигналы.

Рис. 3. Периодический непрерывный сигнал

Сигналы подразделяются на непрерывные и дискретные. На рис.1 слева показан непрерывный сигнал, справа – дискретный. Непрерывные сигналы описываются непрерывными функциями или непрерывными графиками. Дискретные сигналы представляются своими значениями в заданные моменты времени. Такие значения сигналов называют еще отсчетами. Интервалы времени, через которые следуют отсчеты, в общем могут быть постоянными или непостоянными. На практике применяют обычно сигналы с равными (постоянными) интервалами. Если отсчеты сигнала выражены числами определенной разрядности, то такой сигнал называется цифровым или квантованным.

Любой сигнал, как физический процесс, является следствием другого процесса; этот последний является причиной, вызвавшей первый. В данном случае говорят о физической осуществимости сигналов. Причинность, по-другому, каузальность, проявляется в том, что, если сигнал на входе какой-либо системы вызывает отклик в виде другого сигнала на выходе системы, то этот отклик никак не может обнаружиться ранее момента появления первого сигнала на входе этой системы. Для сигналов каузальность проявляется в том, что они всегда имеют начало, что указывает на то, что они вызваны какай-то причиной. Говорят, реальные сигналы каузальны. Каузальные сигналы могут после появления продолжаться ограниченное время или бесконечно долго. Сигналы, длящиеся ограниченное время, называют финитными. При задании финитных сигналов указывают временные моменты их начала и окончания.

В случае применения в качестве несущих сигналов гармонических колебаний при наложении на них исходного сигнала изменяется (модулируется) амплитуда этих колебаний, или частота, или начальная фаза. В первом случае это будет «гармоническое» колебание с переменной амплитудой (рис. 4), во втором - с переменной частотой, в третьем - с переменной начальной фазой. На рис. 4 приведен пример амплитудной модуляции, когда исходный сигнал 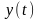формирует модулированный сигнал . Несущий сигнал (без модуляции) представляет собой синусоиду с постоянной амплитудой и постоянной частотой. В результате модуляции модулирующий сигнал изменяет амплитуду синусоиды в соответствии с закономерностью, заложенной в , в результате получается сигнал, приведенный на рис. 4.

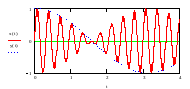
Рис. 4

Модулированные сигналы обладают лучшей помехоустойчивостью, позволяют осуществлять уплотнение каналов связи при передаче их на большие расстояния.

Сигналы, как физические процессы, сопровождаются переносом энергии. Обычно в качестве энергетических характеристик пользуются понятиями энергии сигнала, мгновенной и средней мощности сигнала. Под мгновенной мощностью сигнала понимают количество энергии, переносимой сигналом в единицу времени.

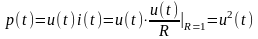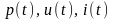
, где - мгновенные значения мощности, напряжении и тока, создаваемые сигналом,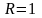 Ом – сопротивление резистора, - время.

Энергию сигнала за некоторый промежуток времени (обычно это время действия сигнала) можно определить по следующей формуле: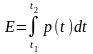 ,где - энергия сигнала,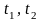 - моменты начала и конца действия сигнала.