1 Предикат

Определение: Пусть даны А и В,

Упорядоченной парой элементов а и в, которые обозначаются , называется пара элементов а и в с указанием порядка этих элементов, т.е. какой из элементов является первым, а какой вторым.

1)

2) (если )

Определение: Прямым произведением множеств А и В называют множество, обозначаемое:

и состоящее из всех упорядоченных пар.

Вида

Очень часто прямое произведение называют декартовым.

Пример:

Действительно:

Замечание:

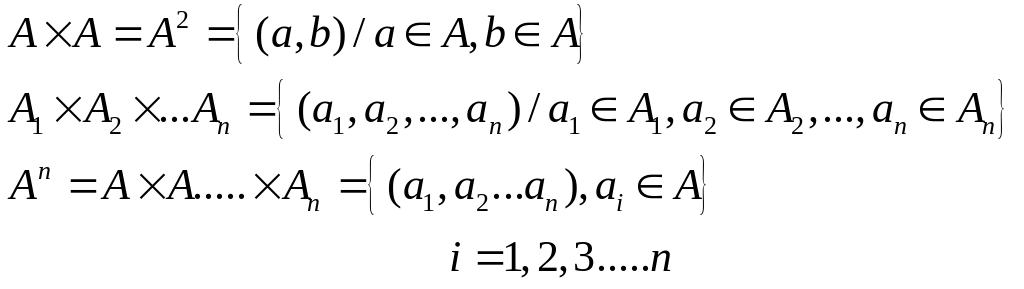
-упорядоченная перестановка, еще ее называют картеж длины n.

Определение: Высказываемой формой или предикатом называют предложение, содержащее переменные и это предложение превращается в высказывание при замене переменных на их значение.

Например: .

- если задан предикат, то всегда указывают множество значений для каждой переменной;

- если в предикате одна переменная, то предикат называют одноместным .

Например:

- область определения предиката:

-область определения предиката

Раз после подстановки вместо переменных из значения предикаты превращаются в высказывание, то над предикатами можно совершать те же логические операции, что и над высказываниями.

2 Логические операции над предикатами

Пусть дан одноместный на А.

Определение: - будем обозначать множество тех и только тех элементов из А, для которых P(x) – истинно. Это множество будем называть областью истинности.

Пример:

Определение: Если , то предикат называют тождественно истинным

, то предикат называют тождественно-ложным.

Пусть - предикат, определяющейся на .

1) Отрицанием называется новый предикат, определенный на А, который истинный для тех и только тех элементов из А, для которых Р(х) – ложно.

Пусть -два предиката на А.

2) Конъюнкция есть новый предикат, определенный на А, область истинности которого состоит из тех и только тех элементов А, для которых оба предиката -истинно.

3) Дизъюнкция есть новый предикат, определенный на А, который истинный хотя бы для одного из данных предикатов.

4) Импликация есть новый предикат, определенный на А, который будет ложен для тех и только тех элементов А, для которых

5) Эквиваленция есть новый предикат, определенный на А, который будет истинный для тех и только тех элементов А, для которых оба предиката либо истинны либо ложны.

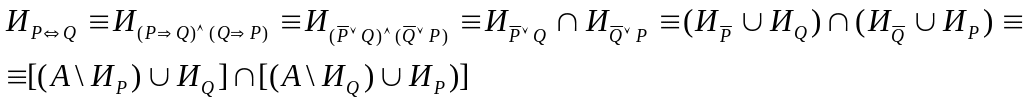
3 Кванторы всеобщности и существования

Р(х) определяется на А

Рассмотрим предложение: «Р(х) истинно для всех х из А»

1. Если Р(х) только истинно, то высказывание – истинно

2. Если Р(х) не только истинно, то это высказывание - ложно

- квантор всеобщности

Переход от предиката Р(х) к высказыванию ( )( ) называют операции навешивания квантора всеобщности

Р(х) определяется на А

Рассмотрим предложение: «Существует х из А, для которого Р(х) - истинно» (это высказывание может быть истинным или ложным)

1. Р(х) – только ложно, то высказывание ложно

2. Р(х) – не только ложно (только истинно или ни тем, ни другим), то высказывание истинно.

- квантор существования

Переход от предиката Р(х) к высказыванию называют операцией навешивания квантора существования.

Кванторы , можно навешивать не только на одноместные предикаты, но на многоместные тоже.

Задача.

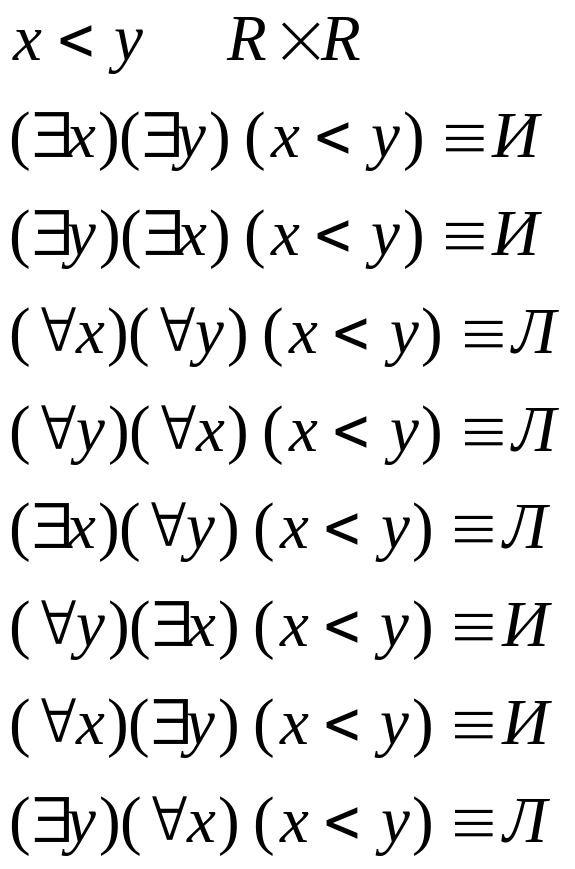
Замечание: Если какая-нибудь переменная находится под знаком квантора, то эта переменная называется связанной.

Если же переменная не находится под знаком квантора, то эта переменная называется свободной.

Пример:

Т.к. , то зависит все от у, есть новый предикат.

Пусть у=1 Пусть у=-1