Раздел: Алгебра Элементы дискретной математики.

Это область математики, занимающаяся изучением свойств дискретных структур, которые возникают как внутри математики, так и в ее приложениях (модели преобразования информации).

Лекция №1.МАТЕМАТИЧЕСКАЯ ЛОГИКА

План:

1) Введение

2) Логические операции

3) Алгебраические формулы

I Введение

Логика – наука о формах и способах человеческого мышления (жен., муж.)

Математическая логика – наука о математических доказательствах с помощью средств

Мат. логика изучает способы правильных умозаключений. Всякая теория состоит из наборов высказывания.

Логическое высказывание – любое повествовательное предложение, в отношении которого можно сказать И оно или Л.

«6 – четное число» - истинное высказывание

«Рим – столица Франции» - ложное высказывание

«Ученик 10 класса» - не высказывание, т.к. неизвестно о ком нужны дополнительные сведения.

«Информатика – интересный предмет» - не высказывание, т.к. «интересный» - неопределенное понятие.

Алгебра логики возникла в середине XIX века в трудах английского математика Джорджа-Буля.

II Логические операции

Будем обозначать высказывания: А, В, С…

* Отрицанием высказывания называется новое высказывание, которое , когда - ложно (выражается словом «не»).

Таблица истинности

И	Л
Л	И

- «Луна – спутник Земли»

- «Луна – не спутник Земли»

* Конъюнкция высказывания А и В ( ) есть новое высказывание, которое И в том и только в том случае, когда оба высказывания А и В – истинны («И» соед.).

И	Л	Л
Л	И	Л
Л	Л	Л
И	И	И

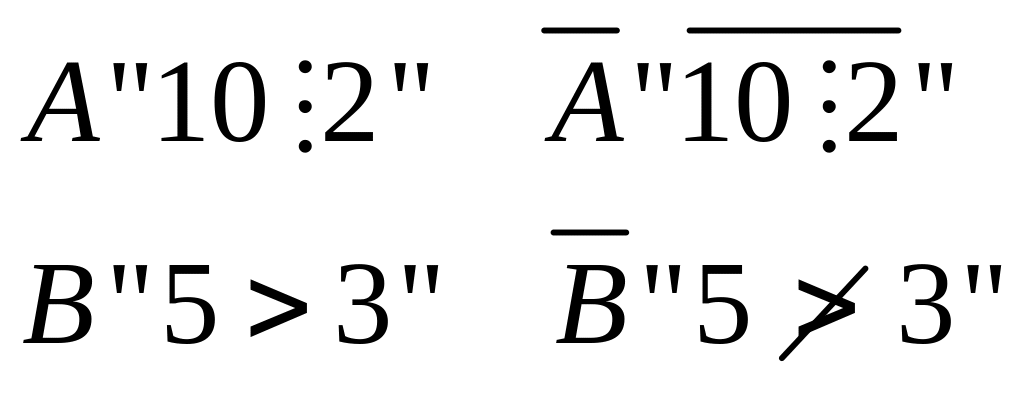
, если

* Дизъюнкция высказывания А и В ( ) есть новое высказывание, которое истинно, когда хотя бы одно из высказываний истинно

* Импликация ( ) есть новое высказывание, которое Л, если А=И, В=Л.

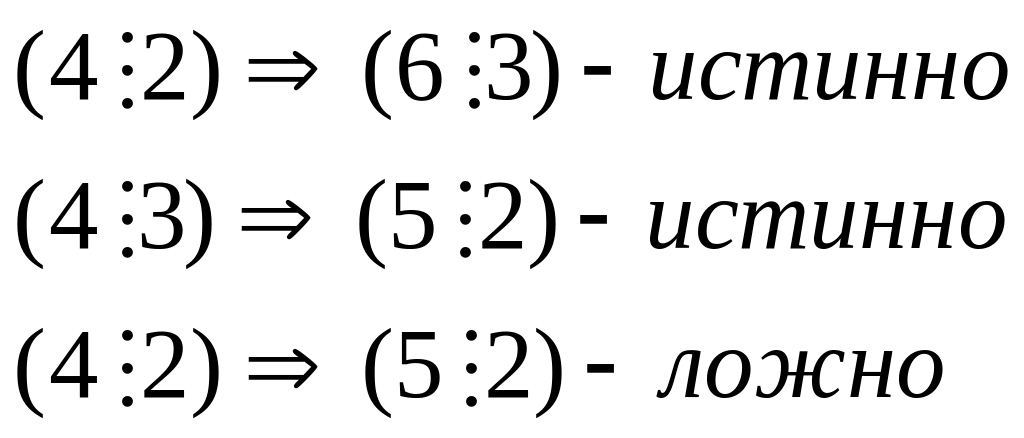
* Эквиваленция ( ) новое высказывание, которое истинно , когда оба А и В – истинны, А и В – ложны.

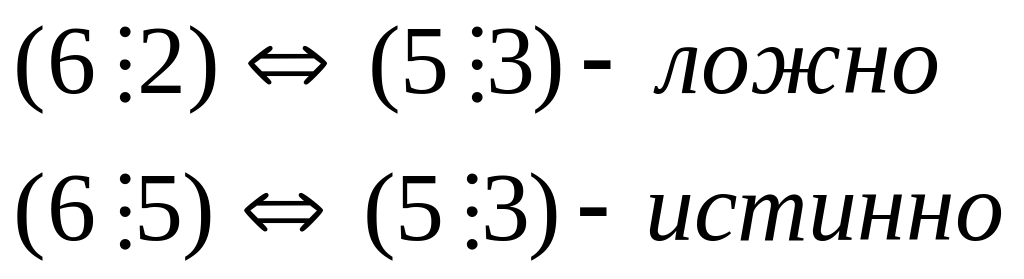
III Формулы

Определение 1: Постоянное высказывание – такое высказывание, значения истинности которого известны.

Определение 2: Высказывания переменны, значения истинности которых не известны.

Определение 3: 1) Все постоянные и переменные высказывания являются формулами;

2) Если А и В – формулы, то так же формулы.

3) Выражения являются формулами в том и только в том случае, если определяются по 1 или 2.

Определение 4: Две формулы алгебры высказывания называются равносильными, если при всяком наборе значений истинности переменных высказываний, входящих в эти формулы, значение истинности этих двух формул совпадают.

Определение 5: Формула называется тождественно истинной или тавтологией, если для всякого набора значений истинности переменных высказываний, входящих в эту формулу, значение истинности всей формулы есть И.

Практика №1.

Доказать:

1)

2)

3)

СВОЙСТВА ЛОГИЧЕСКИХ ОПЕРАЦИЙ
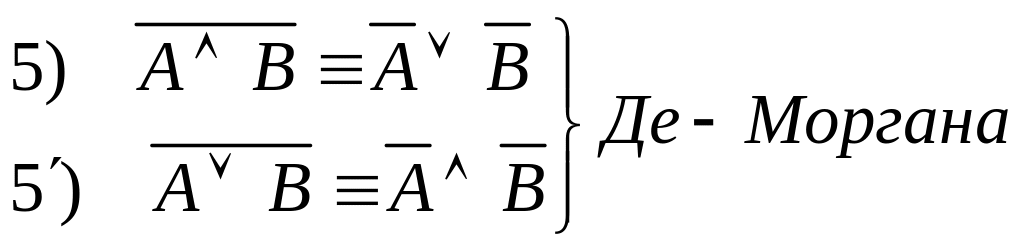