1 Исследование механизма рычажного толкателя

1.1 Динамический синтез механизма

1.1.1 Построение отдельных положений механизма

Для более тщательного исследования механизма разбили движение ведущего звена на 12 положений:

(1.1)

Построение всех положений представлено в приложении 1.

1.1.2 Определение скоростей и точек звеньев

_(1.2)

=1,9*0,12 =0,228м/с

_(1.3)

Для определения скоростей точек и звеньев составили следующие уравнения скоростей:

, .

Построенные планы скоростей представим в приложении 1.

Согласно построенных планов получили:

Рассмотрев треугольник получили:

(1.4)

Из построения нашли значения скоростей точек и звеньев и умножив их на масштабный коэффициент определили их истинное значение.

, , , , , , , , , .

	VC	VD	VF	Vs1	Vs2	Vs3	Vs4	ω2	ω3	ω4
0	0,042	0,037	0,038	0,114	0,114	0,004	0,004	0,315	0,038	0,007
30	0,058	0,052	0,052	0,114	0,0,13 0,13	0,052	0,052	0,23	0,053	0,005
60	0,163	0,16	0,14	0,114	0,196	0,148	0,148	0,13	0,15	0,023
90	0,232	0,22	0,204	0,114	0,228	0,202	0,202	0,02	0,21	0,02
120	0,236	0,202	0.204	0,114	0,224	0,202	0,202	0,16	0,21	0,009
150	0,128	0,116	0,112	0,114	0,156	0,128	0,128	0,26	0,11	0,017
180	0,032	0,028	0,03	0,114	0,118	0,028	0,028	0,3	0,03	0,006
210	0,102	0,092	0,088	0,114	0,144	0,09	0,09	0,27	0,09	0,017
240	0,194	0,175	0,17	0,114	0,202	0,17	0,17	0,17	0,18	0,017
270	0,228	0,206	0,19	0,114	0,228	0,192	0,192	0,0067	0,21	0,0057
300	0,198	0,18	0,178	0,114	0,204	0,176	0,176	0,16	0,18	0,01
330	0,13	0,117	0,118	0,114	0,154	0,116	0,116	0,28	0,12	0,017

Полученные значения скоростей свели в Таблицу 1.1.

Таблица 1.1 Линейные и угловые скорости точек звеньев механизма.

1.1.3 Определение приведенного момента инерции

Для каждого положения механизма приведенный момент инерции находим по формуле:

, (1.5)

(1.6)

где i – номер положения;

m_i – масса соответствующего звена;

­– скорость центра тяжести звена;

i – угловая скорость;

– момент инерции звена;

.

Полученные данные сводим в таблицу 1.2

Таблица 1.2

φ°	Jпр, кг·м2
0; 360 30 60 90 120 150 180 210 240 270 300 330	9,84 9,59 10,23 11,1 11,1 10,13 9,78 9.48 10,6 10,87 10,28 10,23

1.1.4 Определение приведенного момента сил сопротивления

Приведенный момент сил сопротивления

, (1.7)

где - приведенный момент сил тяжести,

, (1.8)

где – сила тяжести звена;

i – номер положения;

–скорость центра тяжести звена;

cosα – угол между силой тяжести звена и центра тяжести звена.

В нашем случае имеем:

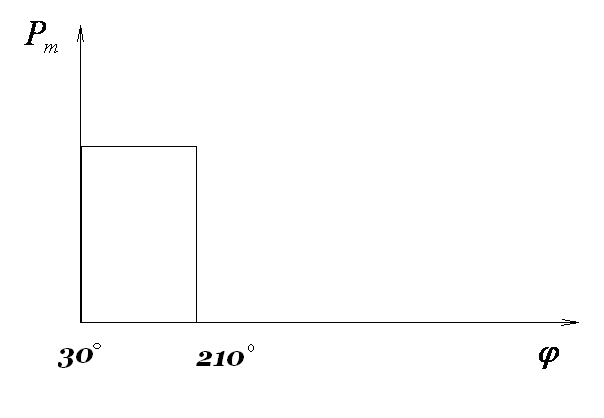
- момент от нагрузки, значение берем из графика 1

, (1.9)

График 1

Полученные данные сводим в таблицу 1.3

Таблица 1.3

φ, град	0	30	60	90	120	150	180	210	240	270	300	330
, Н∙м	22,84	23,25	15,33	4,25	-8,8	-25,84	-26,98	-9,95	-7,63	2,21	9,93	34,7
, Н∙м	0	32,84	88,42	128,84	128,84	70,75	19	55,6	0	0	0	0
, Н∙м	22,84	56,1	103,75	133,1	120,04	44,89	-8,03	45,6	-7,63	2,21	9,93	34,7

1.1.5 Определение работы сил движущих и сил сопротивления.

(1.10)

В нашем случае имеем:

, (1.11)

где i – номер положения;

Δφ – приращение угла;

– приведённый момент сил сопротивления;

– работа сил сопротивления

радиан

Полагаем, что момент сил движущих есть величина постоянная (const)

(1.12)

(1.13)

где M_д – приведенный момент сил движущих;

A_д – работа сил движущих;

Δφ – изменение угла поворота.

Изменение кинетической энергии определяется по формуле

(1.14)

Значения работы сил сопротивления, работы сил движущих, изменения кинетической энергии для всех положений механизма сводим в таблицу 1.4

Таблица 1.4

Положение J	0	30	60	90	120	150	180	210	240	270	300	330
,Дж	0	20,6	62,4	124,34	190,54	233,67	243,31	253,13	263,1	261,7	264,73	276.26
,Дж	0	24,3	48,6	72,9	97,2	121,5	145,3	169,6	193,9	218,3	242,3	2666
,Дж	0	3,7	-13,8	-51,44	-93,4	-112,7	-98,01	-83,53	-69,2	-43,5	-22,4	-9,7

1.1.6 Определение момента инерции маховика

Момент инерции маховика

, (1.15)

где – максимальный момент инерции;

, (1.16)

где δ – неравномерность хода;

ΔJ_пр – изменение приведенного момента инерции;

, (1.17)

изменение кинетической энергии:

, (1.18)

Примем радиус маховика за 0,5 м, тогда его масса равна:

_(1.19)

1.2 Динамический анализ механизма

1.2.1 Определение истинного закона движения механизма

Для определения истинного закона движения рассмотрим дифференциальное уравнение движения, которое имеет следующий вид:

(1.20)

где – приведённый момент сил сопротивления;

– приведённый момент сил движущих;

– момент инерции;

– изменение момента инерции от угла поворота.

(1.21)

Полученные значения производной сведём в таблицу 1.5.

Таблица 1.5 Значения производной приведённого момента инерции

Положение	0	30	60	90	120	150	180	210	240	270	300	330
Јпрj, Кг*м2	-0,48	1,22	1,66	0	-1,85	0,67	-0,57	2,14	0,52	-1,13	-0,095	-0,75

Решается дифференциальное уравнение методом последовательных приближений с помощью начальных условий. В основу решения положена формула равноускоренного движения. Полагаем, что в пределах достаточно малого угла поворота машина движется равноускоренно. Тогда, используя начальные условия, получим

Зная , определяются

Зная определяем .

Из дифференциального уравнения выражаем ε_i .

(1.22)

Зная ε_i , можно найти ω в следующем положении

Расчет вести до установившегося движения, то есть когда закон движения из цикла в цикл повторяется. Данные для установившегося движения представлены в приложении 1.