Лекция№4 Функция. Последовательность как функция натурального аргумента. Пределы последовательностей. Виды неопределенностей. Числовые промежутки. Окрестность точки.

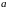Пусть и 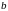- действительные числа, причем .

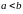Числовыми промежутками (интервалами) называют подмножества всех действительных чисел, имеющих следующий вид:

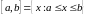- отрезок (замкнутый промежуток)

- интервал (открытый промежуток)

-

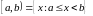полуоткрытые интервалы

-

,

,

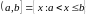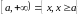
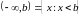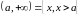
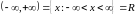
- бесконечные интервалы.

Числа 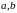- называются соответственно левым и правым концом промежутков. Символы 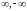это не числа, это символическое обозначение процесса неограниченного удаления точек числовой оси от начала 0 влево и вправо.

Давайте введем понятие окрестности точки.

Определение: Пусть 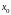- любое действительное число (точка на действительной прямой). Окрестностью точки называется любой интервал 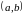, содержащий точку .

Определение: Интервал 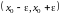, где 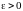называется - окрестностью точки . Число - центром, а число - радиусом окрестности.

Если 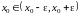, то выполняется неравенство 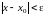выполнение этого неравенства означает попадание точки в - окрестность точки .

Понятие функции

Одним из основных математических понятий является понятие функции. Понятие функции связано с установлением зависимости (связи) между элементами двух множеств. Пусть даны два непустых множества X и Y .

Определение: Соответствие f , которое каждому элементу 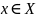сопоставляет один и только один элемент 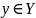называется функцией и записывается 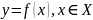или .

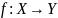Говорят еще, что функция 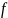отображает множество 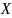на множество .

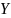Множество называется областью определения функции и обозначается .

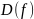Множество всех называется областью значений функции и обозначается .

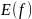Числовые функции

Пусть задана функция

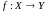
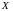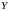Если элементами множеств и являются действительные числа, т.е. , то функцию 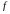- называют числовой функцией. В дальнейшем будем изучать только числовые функции, для краткости будем называть их просто функциями.

- аргумент (независимая переменная);

- значение функции или (зависимая переменная).

Графиком функции называется множество всех точек плоскости 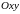, для каждой из которых является значением аргумента, а - соответствующим значением функции.

Способы задания функций

Наиболее часто встречается 3 способа задания функций:

1. Аналитический - функция задается в виде одной или нескольких формул.

Пример:

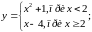
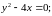
2. Графический способ: задается график функции

3. Табличный способ: функция задается таблицей ряда значений аргумента и соответствующих значений функции.

Пример: известные таблицы значений тригонометрических функций, логарифмические функции.

Обратная функция

Пусть задана функция 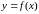с областью определения 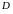и областью значений .

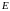Если каждому значению 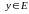соответствует единственное значение 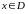, то определена функция с областью определения и множеством значений .

Такая функция называется обратной к функции .

Записывается .

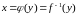Про функции и говорят, что они являются взаимно обратными.

Примеры:

1) 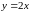, обратная

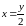
2) 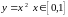, обратной является

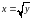
3) Для функции 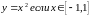обратной не существует, т.к. одному значению соответствует два значения .

Из определения обратной функции вытекает, что функция имеет обратную, тогда и только тогда, когда функция задает взаимно- однозначное соответствие между множествами и .

Замечание: Графики взаимно обратных функций и симметричны относительно биссектрисы первого и третьего координатных углов.