2. Подходы к оценке показателей роста

Самым важным элементом входных данных при оценке, особенно, быстрорастущий организаций, являются темпы роста, используемые для предсказания будущих показателей.

Существуют три основных способа оценки роста любой организации.

Одни из них – это изучение роста на основе прошлых доходов – ее исторических темпов роста. Такой подход может оказаться полезным при оценке устойчивых фирм, а для быстрорастущих ее применение представляет опасность.

Во-вторых, можно довериться аналитикам, выдающим корректировочные оценки роста предприятий, и использовать эти показатели при определении ценности.

В-третьих, можно оценить рост организации, основываясь на ее фундаментальных показателях. Рост организации, в конечном счете, определяется объемом ее реинвестирования в новые активы и качеством этих инвестиций. При этом инвестиции определяют достаточно широко, чтобы включить создание каналов распределения продукции, расширение возможностей маркетинга. Оценивая эти входные данные, в каком-то смысле, вы оцениваете фундаментальные темпы роста организации.

1. Оценка исторического роста.

   1. Арифметическое и геометрическое среднее

Среднеарифметическое – это простое среднее прошлых темпов роста показателя. Среднегеометрическое учитывает сложный процент, накапливаемый от периода к периоду.

,

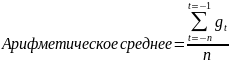где, 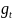- темпы роста в год t.

,

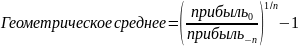где, 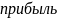– прибыль в год t.

Геометрическое среднее – более точная мера истинного роста прибыли в прошлом, особенно, если рост претерпевал сильные изменения год от года.

Пример. Даны показали выручки, EBITDA и EBIT и чистый доход компании за 6 лет. Рассчитайте арифметические и геометрические темпы роста этих показателей, а также стандартное отклонение по ежегодным процентным отклонениям (показателям роста). Сделайте выводы о целесообразности применения этих методик на различных показателях.

Таблица 10 - Показатели эффективности деятельности организации

Год	Выручка	EBITDA	EBIT	ЧД
1	22245	4551	2604	1560
2	27037	4850	2931	1781
3	27973	4268	1960	1154
4	29794	4276	1947	1180
5	29398	3019	822	212
6	30931	5398	3216	817

2. Модели линейной и логарифмически-линейной регрессии

Рассмотрим применение регрессионного аппарата на временном ряде прибыли на одну акцию.

Линейная регрессия этой модели записывается следующим образом

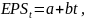
где 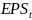– прибыль на акцию в период t, t – временной период.

Коэффициент наклона при временной переменной является мерой изменения прибыли за временной период. Проблема с линейной моделью состоит в том, что она определяет рост в единицах прибыли на акцию и не годиться для прогнозирования будущего роста с учетом сложных процентов.

Логарифмически-линейная версия этой модели преобразовывает коэффициент в процентное измерение:

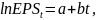
где 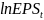– натуральный логарифм прибыль на акцию в период t, t – временной период.

Коэффициент регрессии становиться мерой процентного изменения прибыли на единицу времени.

В таблице приведена прибыль на акцию за 10 лет компании. Используя приведенные выше методики оценки роста, подсчитайте темп роста среднегодовой темп роста прибыли на акцию.

Таблица 11 – Линейная и логарифмически-линейная модели роста

на примере компании

Год	Прибыль на 1 акцию	Процентное изменение	Ln(
1	0,42
2	0,41
3	0,40
4	0,58
5	0,65
6	0,72
7	0,82
8	0,93
9	1,07
10	1,24