Рекомендации студентам по изучению читаемых дисциплин кафедрой сам в октябре 2014 года

1.	Курс	4 курс бакалавры (гр. САУ-11)
2.	Название дисциплины	«Теория принятия решений»
3.	ФИО лектора	доц. Селякова С.М.
4.	ФИО ассистента	доц. Селякова С.М.
5.	Задание	Тема 1: «Методы обработки экспертной информации». Лабораторная работа № 1, №2.
6.	Варианты заданий	в электронном источнике библиотеки ДонНТУ: Методичні вказівки до виконання лабораторних робіт по темі "Методи обробки експертної інформації" з дисципліни "Теорія прийняття рішень"
7.	Срок выполнения	Лабораторная работа №1 – третья неделю октября 2014 г., Лабораторная работа №2 – четвертая неделя октября 2014 г.
8.	Лекционный материал	См. ниже
9.	Литература	Рыков А.С. Модели и методы системного анализа: принятие решений и оптимизация: Учебное пособие для вузов / Рыков А.С. – М.: МИСИС, Издательский дом «Руда и металлы», 2005. – 352 с.
10.	Время консультаций	вторник, с 12.00-14.00, ауд. 10.324
12.	Форма сдачи	Электронный вариант выполненного задания отправить на адрес преподавателя svemisel@gmail.com либо печатный или рукописный вариант – на кафедру (10.318)
13.	Контакты (e-mail, skype)	e-mail – sam_dntu@i.ua, svemisel@gmail.com

1. Теоретична частина

1. Ранжирування альтернатив

Припустимо, що є кінцева кількість вимірюваних альтернатив , сформульовані показники порівняння (критерії) , по яким здійснюється порівняння альтернатив.

Ранжирування являє собою процедуру упорядкування альтернатив, що виконується експертом в шкалі порядку. На основі своїх знань і досвіду експерт розподіляє об'єкти в порядку переваги, керуючись одним або декількома показниками порівняння.

Сутність процедури ранжирування полягає в наступному. При ранжируванні експерт повинен розташувати альтернативи в порядку, який представляється йому найбільш раціональним, і приписати кожної з них числа натурального ряду – ранги. При цьому ранг 1 отримує найкраща альтернатива, а ранг – найгірша альтернатива.

Якщо серед альтернатив немає однакових за порівнюваними показниками, тобто немає еквівалентних альтернатив, то експерт складає упорядковану послідовність: , де – найкраща альтернатива; – менш краща ніж , але має більшу перевагу над альтернативами, що залишилися і т.п.

Еквівалентні альтернативи позначаються знаком . Еквівалентним альтернативам присвоюють так звані пов'язані ранги, значення яких визначаються як середнє від суми місць, поділених між собою альтернативами з однаковими рангами.

Наприклад, для ряду ранги дорівнюють наступним значенням:

,

.

Таким чином, сума рангів, що отримується в результаті ранжирування альтернатив, буде дорівнювати сумі чисел натурального ряду .

Під час групового експертного оцінювання кожний -й експерт присвоює кожній -й альтернативі ранг У результаті проведення експертного оцінювання виходить матриця рангів , , з розмірністю , де – кількість експертів; – кількість альтернатив. Для кожної альтернативи розраховують суму рангів:

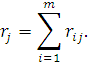
Потім, виходячи з величини встановлюють результуючий ранг для кожної альтернативи. Найвищій (перший) ранг присвоюють альтернативі, що має найменшу суму рангів, і навпаки, альтернативі, що має найбільшу суму рангів, присвоюють самий низький ранг. Інші альтернативи впорядковують у відповідності зі значенням суми рангів відносно альтернативи, якій присвоюється перший ранг.