Вариант 8
1. Вычислить предел функции:
а)
; б)
.
2. Вычислить производную функции:
а)
; б)
; в)
.
3. Исследовать функцию и построить её график
.
Найдите интегралы:
а)
;
б)
;
в)
.
5. Вычислите площадь фигуры, ограниченной графиками функций и .
;
.
6. Найдите общее решение дифференциального уравнения
.
7. Напишите первые пять членов ряда
.
8. Выполняется ли необходимый признак сходимости ряда?
9. Исследуйте на сходимость ряд по признаку Даламбера.
.
Вариант 9
1. Вычислить предел функции:
а)
; б)
.
2. Вычислить производную функции:
а)
; б)
; в)
.
3. Исследовать функцию и построить её график
.
4. Найдите интегралы:
а)
;
б)
;
в)
.
5. Вычислите площадь фигуры, ограниченной графиками функций и .
;
.
6. Найдите общее решение дифференциального уравнения
.
7. Напишите первые пять членов ряда
.
8. Выполняется ли необходимый признак сходимости ряда?
9. Исследуйте на сходимость ряд по признаку Даламбера.
.
ВОПРОСЫ К ЭКЗАМЕНУ
Основные теоремы о пределах.
Предел отношений синуса дуги к самой дуге.
Сравнение бесконечно малых.
Непрерывность функции.
Свойства функций, непрерывность на сегменте.
Задачи, приводящие к понятию производной.
Определение производной.
Производная суммы, производная произведения.
Производная частного.
Производные
,
,
,
.Производные
,
,
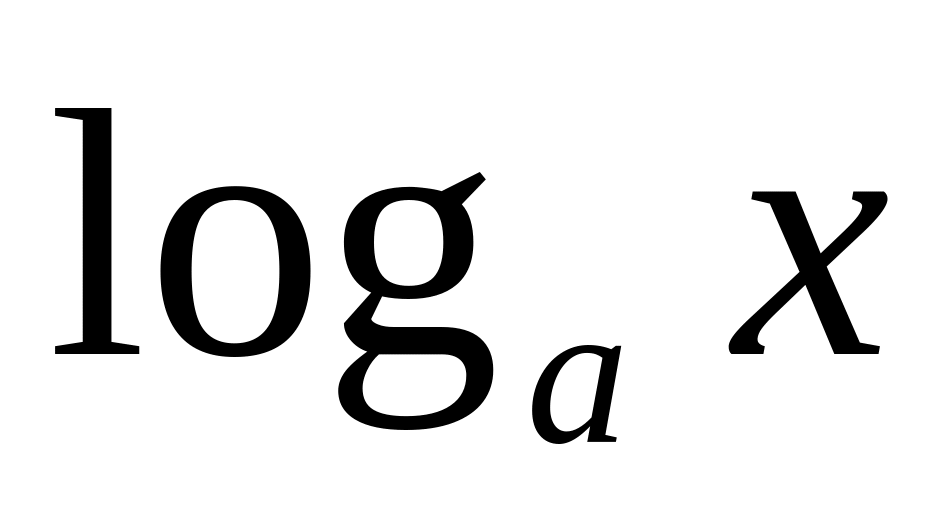.Производные
,
,
,
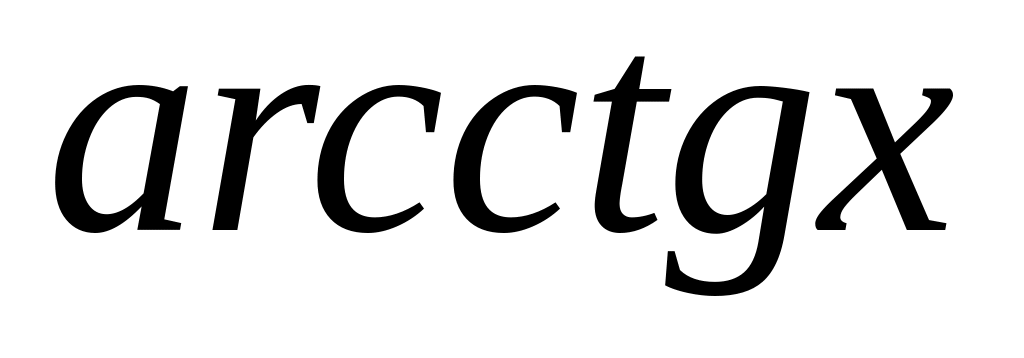.Дифференциал функции. Таблица формул для дифференцирования.
Производные и дифференциалы высших порядков.
Правило Лопиталя.
Возрастание и убывание функций.
Максимумы и минимумы.
Наибольшее и наименьшее значения функции на отрезке.
Выпуклость и вогнутость функции. Точки перегиба.
Построение графика функции. Схема построения.
Понятие первообразной функции и неопределённый интеграл.
Свойства неопределённого интеграла.
Таблица неопределённых основных интегралов.
Интегрирование по частям.
Задача, приводящая к понятию определённого интеграла.
Понятие определённого интеграла.
Свойства определённого интеграла. Формула Ньютона-Лейбница.
Обыкновенные дифференциальные уравнения.
Необходимый признак сходимости рядов.(liman=0)
Признак Даламбера.
Библиографический список
а) основная учебная литература:
Баврин, Иван Иванович. Математика (текст): учебник для вузов /И.И.Баврин.-10-е изд., стер.-М.: Академия, 2013,-619с.: рис., табл.
Хуснутдинов Р.Ш., Жихарев В.А. Математика для экономистов в примерах и задачах. Изд-во Лань, 2012 http://e.lanbook.com/books/element.php?pl1_cid=25&pl1_id=4233
Высшая математика в упражнениях и задачах. В 2 ч. [Текст] : учеб. пособие. Ч. 1 / П. Е. Данко [и др.]; [отв. ред. О. А. Богатырева и др.]. - 7-е изд., испр. . - М. : Мир и Образование. - [Б. м.] : Астрель. - [Б. м.] : Оникс, 2012. - 368 с.
Высшая математика в упражнениях и задачах. В 2 ч. [Текст] : учеб. пособие. Ч. 2 / П. Е. Данко [и др.] ; [отв. ред. О. А. Богатырева и др.]. - 7-е изд. испр. - М. : Мир и Образование. - [Б. м.] : Астрель. - [Б. м.] : Оникс, 2012. - 448 с..
Берман П.М. Решебник к сборнику задач по курсу математического анализа Изд-во Лань, 2011 http://e.lanbook.com/books/element.php?pl1_cid=25&pl1_id=674
б) дополнительная учебная литература:
Красс М. С. Математика для экономистов [Текст] / М. С. Красс, Б. П. Чупрынов. - СПб. : Питер, 2009. - 464 с.
Мышкис А.Д. Лекции по высшей математике Изд-во Лань, 2009.- 608с. http://e.lanbook.com/books/element.php?pl1_cid=258pl1_id=281 (эл)
Красс М. С. Математика для экономистов [Текст] : учеб. пособие / М. С. Красс, Б. П. Чупрынов. - Санкт-Петербург : Питер, 2005. - 464 с.
Красс М.С. Математика для экономистов [Текст] / М. С. Красс, Б. П. Чупрынов. - СПб. : Питер, 2008. - 461 с.
Данко, П. Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 1: учеб. пособие для вузов/ П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. – М.: Оникс 21 в.: Мир и Образование, 2005. – 304 с.
Данко, П. Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 2: учеб. пособие для вузов/ П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. – М.: Оникс 21 в.: Мир и Образование, 2005. – 416 с.
Берман Г.Н. Сборник задач по курсу математического анализа. – СПБ.: Профессия, 2003.
Бугров Я.С., Никольский С.М. Высшая математика: задачник. М., Физматлит, 2001. М., Дрофа, 2004.
Демидович Б.П.Задачи и упражнения по математическому анализу для ВТУЗОВ., М., ИНТЕГРАЛ-ПРЕСС, 1997.
Ильин В.А., Позняк Э.Г. Основы математического анализа. Ч.1,2. – М.: Физматлит, 2002.
Кудрявцев Л.Д. Курс математического анализа. Т.1,2. - М.: Дрофа, 2003.
Минорский В.П. Сборник задач по высшей математике. М., Физматлит, 2003.
Никольский С.М. Курс математического анализа. Т.1,2. – М.: Высшая школа, 1990.
Сборник задач по высшей математике для экономистов: Учебное пособие / Под ред. В.И. Ермакова.- М.: ИНФРА-М, 2002.
Сборник задач по математике для ВУЗов. Под ред. Ефимова А.В., Поспелова А.С. М., Физматлит, ч. 1-4, 2001-2004.
Гусак А.А. Высшая математика. Т. 1, 2. – Минск, изд. Тетра Системс, 1998
Смирнов В.И. Курс высшей математики. М.: Наука, 1980.
Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т.1,2,3. – М.: Физматлит, 2003.
Высшая математика для экономистов : учебник для вузов / Н. Ш. Кремер и др., ред. Н. Ш. Кремер. - 2-е изд., перераб. и доп. - М. Юнити, 2004. - 471 с.
Минорский, В.П. Сборник задач по высшей математике/ В.П.Минорский, изд. 15-е., М.: Физматлит, 2006. – 336с. http://edu-lib.net/matematika-2/dlya-studentov/minorskiy-v-p-sbornik-zadach-po-vyisshey-m
Мышкис А.Д. Лекции по высшей математике Изд-во Лань, 2009.- 608с. http://e.lanbook.com/books/element.php?pl1_cid=258pl1_id=281 (эл)