Понятие определённого интеграла

Определённым интегралом от непрерывной функции на отрезке называется приращение какой-нибудь её первообразной на этом отрезке.

.

Эта формула называется формулой Ньютона – Лейбница.

В отличие от неопределенного интеграла определённый интеграл есть число. Геометрический смысл определённого интеграла состоит в том, что он численно равен площади фигуры, образованной подынтегральной функцией, и прямыми , , .

Пример

Вычислить площадь фигуры, ограниченной параболой и прямой .

Сделаем чертёж. Для этого определим вершину параболы: .

Найдём точки пересечения параболы и прямой:

Теперь вычислим исходную площадь:

(кв. ед.)

Дифференциальные уравнения первого порядка с разделяющимися переменными

Дифференциальным уравнением первого порядка с разделяющимися переменными называется уравнение вида

.

Это наиболее простой тип дифференциальных уравнений. Решается методом разделения переменных, так чтобы при была функция от , а при была функция от .

Пример

Проинтегрировать уравнение:

.

Решение

Преобразуем:

.

Разделим переменные, поделив на :

.

Проинтегрируем:

,

,

; .

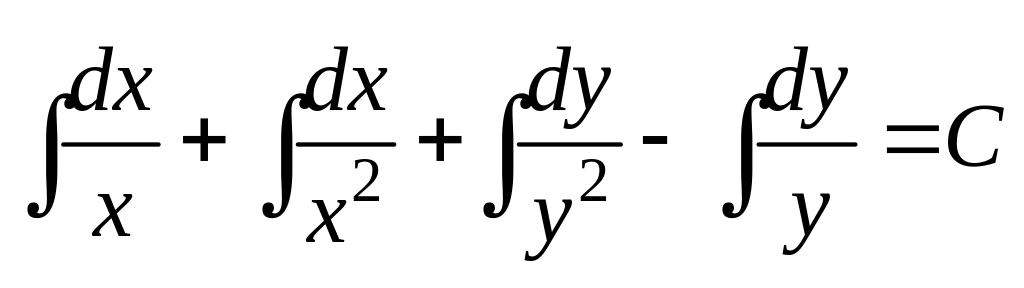Замечание Непосредственной проверкой можно убедиться, что и являются решениями данного дифференциального уравнения, однако, они не получаются из общего интеграла ни при каком значении С. Следовательно, в ходе решения были потеряны интегральные кривые и (оси координат). Эта потеря произошла в том месте, где разделили на .

Ряды

а) основные понятия

Пусть задана бесконечная последовательность чисел .

Числовым рядом называется составленное из этих чисел выражение

.

Числа называются членами ряда, - общим членом ряда.

Конечная сумма

называется -ой частной суммой ряда.

Если существует конечный предел , ряд называется, сходящимся, в противном случае – расходящимся. Если ряд сходится, число называется суммой ряда, а разность называется остатком ряда.

Пример

По заданному общему члену записать пять первых членов ряда.

Решение:

Давая последовательно значения 1, 2, 3, 4, 5, получим

;

.

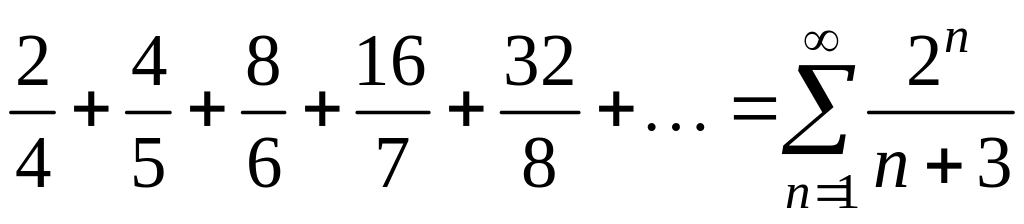б) необходимый признак сходимости

Если ряд сходится, то его общий член стремится к нулю при . Отсюда следует, что если не стремится к нулю, то ряд расходится.

Пример

Установить, выполняется ли необходимый признак сходимости ряда

.

Решение

Общий член ряда .

, необходимое условие сходимости ряда не выполняется, и следовательно, этот ряд расходится.

в) признак сходимости Даламбера

Если ряд с положительными членами таков, что существует

,

то при ряд сходится, а при ряд расходится, при , вопрос о поведении ряда остаётся открытым.

Пример

Исследовать на сходимость ряд

.

Решение

Здесь , , поэтому

,

следовательно, ряд сходится.

Контрольная работа № 1 Вариант 0

1. Вычислить предел функции:

а) ; б) .

2. Вычислить производную функции:

а) ; б) ; в) .

3. Исследовать функцию и построить её график

.

4. Найдите интегралы:

а) ;

б) ;

в) .

5. Вычислите площадь фигуры, ограниченной графиками функций и .

; .

6. Найдите общее решение дифференциального уравнения

.

7. Напишите первые пять членов ряда

.

8. Выполняется ли необходимый признак сходимости ряда?

9. Исследуйте на сходимость ряд по признаку Даламбера.

.