Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Кемеровский государственный университет»

Кафедра высшей математики

Математический анализ для студентов экономического факультета (озо, 1 курс)

Кемерово 2014

Составитель: к.п.н., доцент В. Ю. Сафонова

Правила и порядок выполнения контрольных работ

1. Не следует приступать к выполнению контрольной работы до решения достаточного количества задач по учебному материалу, соответствующему этому заданию.

2. Каждую контрольную работу следует выполнять в отдельной тетради, чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента.

3. На обложке тетради должны быть разборчиво написаны фамилия, имя и отчество студента, факультет, номер группы, название дисциплины, номер контрольной работы, номер варианта. В конце работы следует поставить дату её выполнения и расписаться.

4. Номер варианта контрольной работы, которую выполняет студент, должен совпадать с последней цифрой номера его зачётной книжки.

5. Решения задач надо располагать в порядке возрастания номеров. Условия задач следует переписать в тетрадь.

6. При решении задач нужно обосновывать каждый этап решения, исходя из теоретических положений курса.

Решение задач и примеров следует излагать подробно, объясняя все выполненные действия и используемые формулы.

Полученный ответ следует проверить способами, вытекающими из существа данной задачи.

Предел функции

При вычислении пределов следует учитывать:

1. Для того, чтобы число А было пределом функции при , необходимо и достаточно, чтобы эта функция была представима в виде:

,

где - бесконечно малая.

2. Предел постоянной величины равен самой постоянной:

, С – const.

3. Предел суммы (разности) функций равен сумме (разности) пределов слагаемых:

.

4. Предел произведения функций равен произведению пределов сомножителей:

.

5. Предел отношения двух функций равен отношению пределов этих функций:

.

6. Если функция имеет предел при , то

.

7. Постоянный множитель можно выносить за знак предела:

, С – const.

8. Для непрерывных функций символы предела и функции можно поменять местами:

.

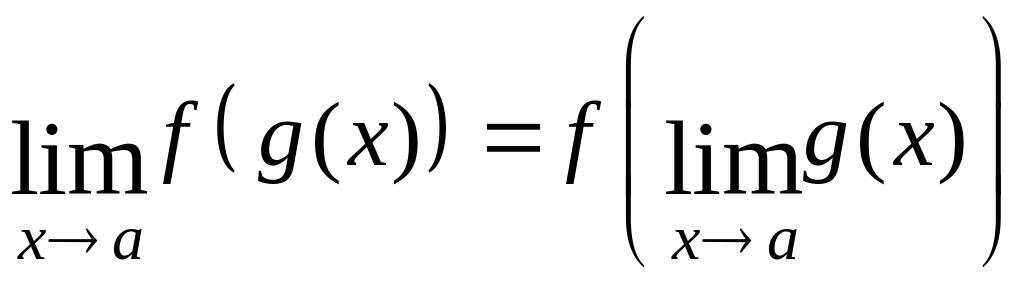В простейших случаях нахождение предела сводится к подстановке в данное выражение предельного значения аргумента.

Например:

.

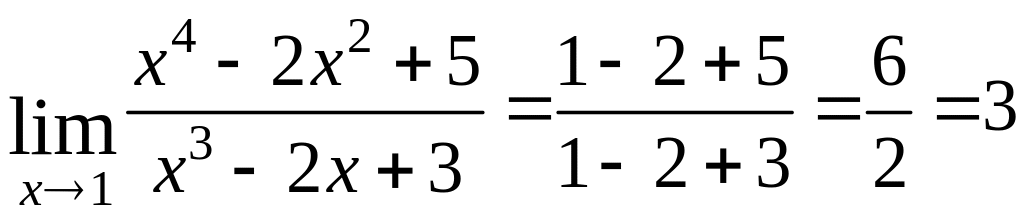Это не всегда возможно. Нахождение предела функции следует начинать с подстановки значения в выражение для функции. При этом, если получается числовое значение или , то искомый предел найден.

Если получается неопределённое выражение, то для нахождения предела нужно преобразовать функцию так, чтобы раскрыть эту неопределённость.

Например:

а) вычислить предел

.

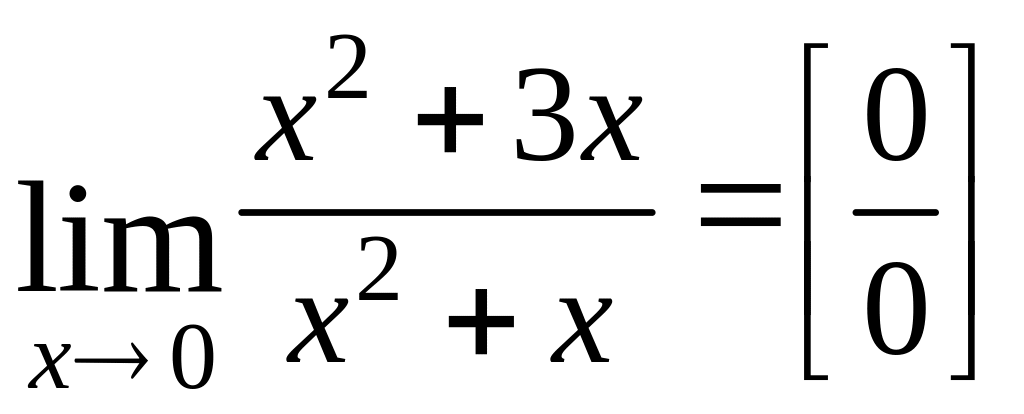Разложим и числитель, и знаменатель на множители:

.

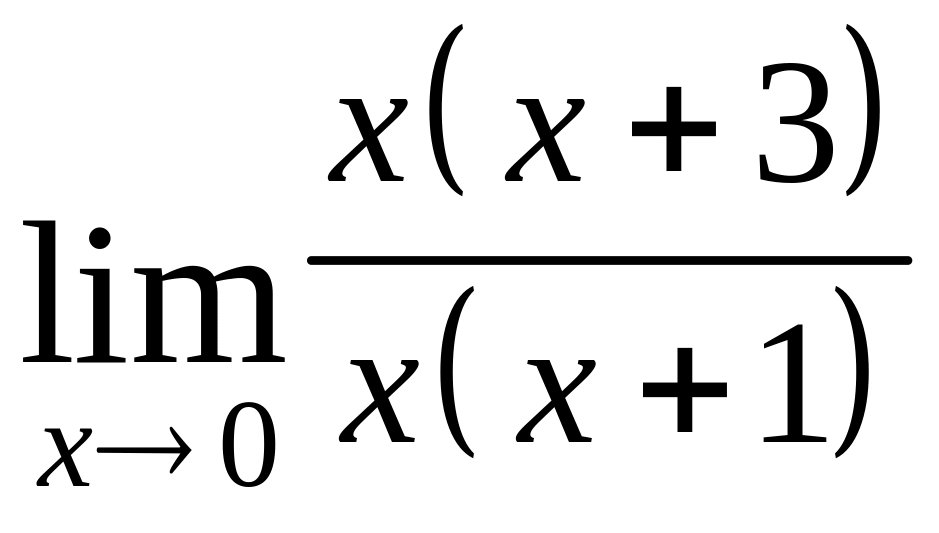Сократим на общий множитель и получим:

.

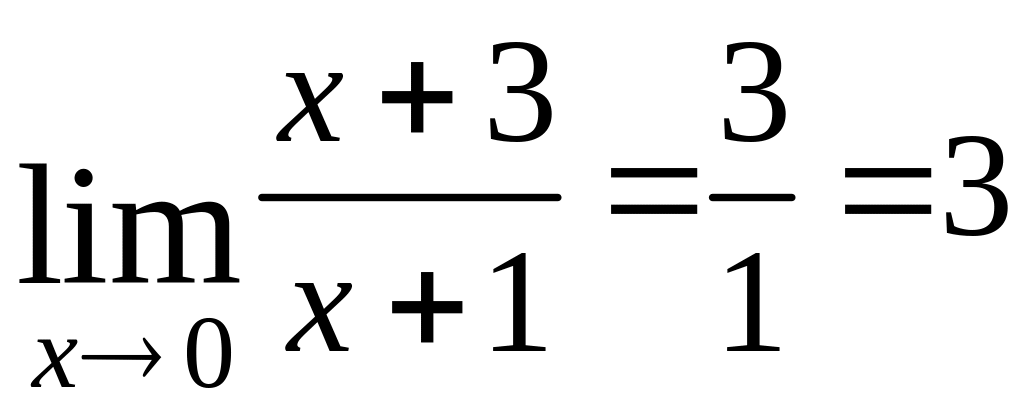б) вычислить предел

.

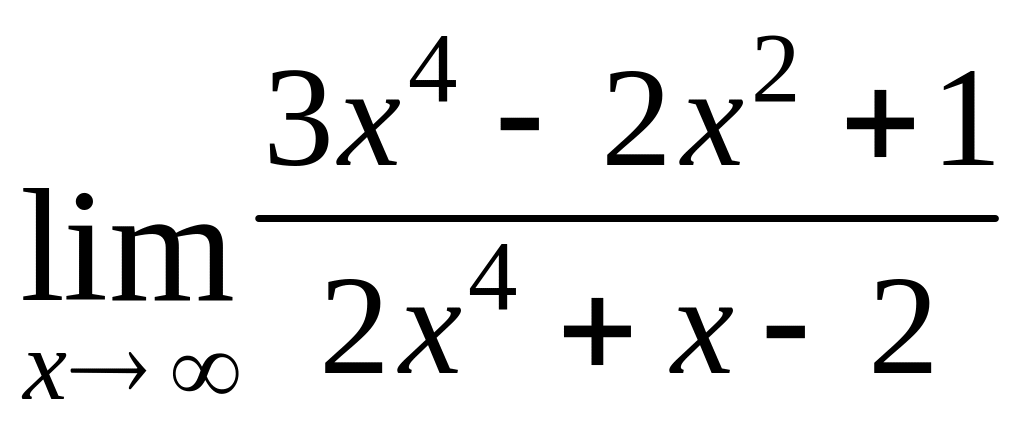Получаем неопределённость .

В этом случае для вычисления предела и числитель, и знаменатель делим на в старшей степени.

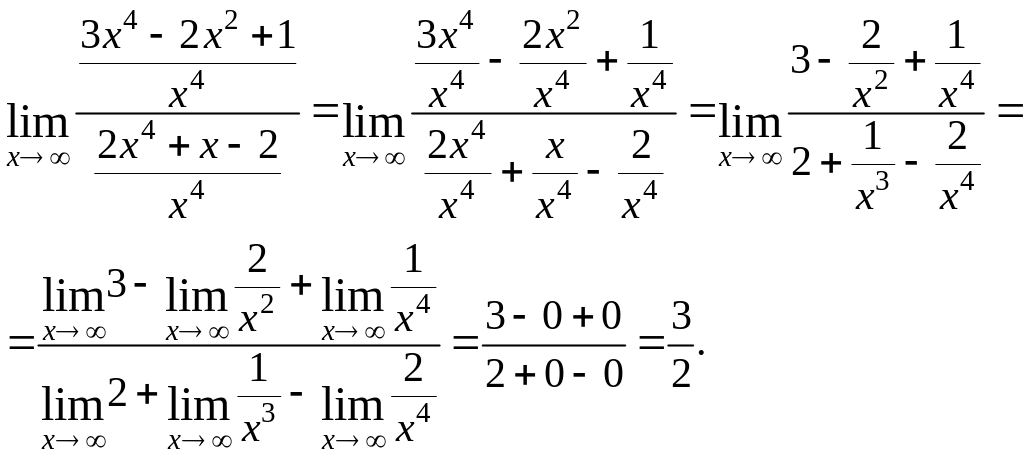
Правила дифференцирования функций и производные элементарных функций

Пусть и - две функции аргумента , имеющие производные и . Тогда:

1) ;

2) ;

3) ;

4) ;

5) ;

6) Если сложная функция, т. е. , а , то производная находится, как ;

7) ;

8) ;

9) ;

10) ;

11) ;

12) ;

13) ;

14) ;

15) ;

16) ;

17) ;

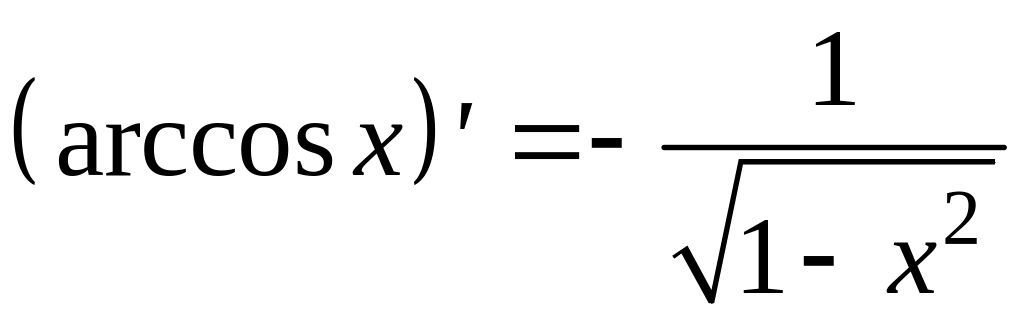18) ;

19) .

Например:

найти производные функций:

а) :

= .

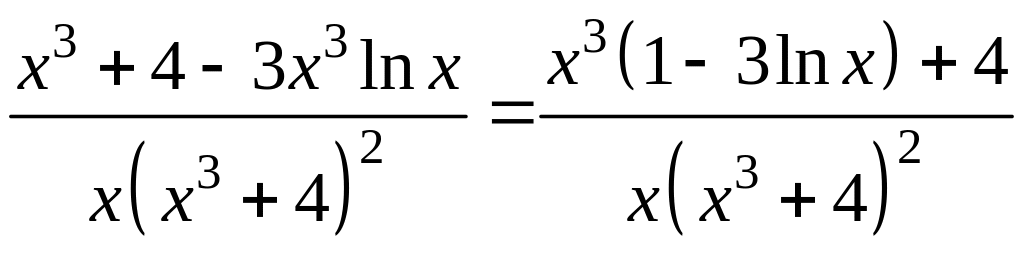б) :

;

в) :

.
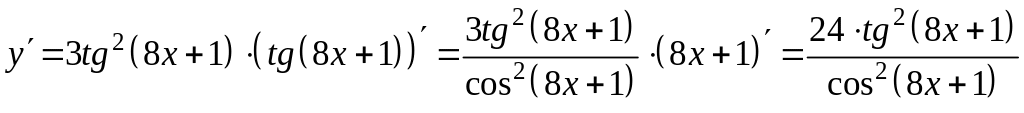