6.5 Вплив температури на швидкість реакцій

На основі експериментальних досліджень шведський дослідник С.Арреніус вивів рівняння:

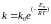(6.1)

де k – константа швидкості реакції;

k_o – стеричний множник;

e – основа натурального логарифма;

E_a – енергія активації, для хімічних реакцій 40-400 кДж/моль.

Якщо при зміні температури концентрація реагентів залишається постійною, то залежність швидкості реакції від температури опишеться рівнянням:

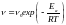(6.2)

Прологарифмувавши рівняння (1), одержимо:

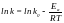
Рівняння Арреніуса дає можливість одержати більш точні розрахунки зміни швидкості реакції зі збільшенням температури, ніж рівняння Вант-Гоффа. Правило Вант-Гоффа спостерігається для обмеженої кількості реакцій, які протікають при температурах, близьких до кімнатних.

Отже, константа швидкості (а при постійний концентраціях і швидкість реакції) росте зі збільшенням температури по експоненційному закону. У відповідності з рівнянням Арреніуса константа швидкості реакції зменшується з ростом енергії активації. Рівняння Арреніуса дає змогу розраховувати константи швидкості (і швидкості) реакції при різних температурах.

Наприклад, для двох температур

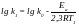
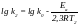
Віднімаючи від другого перше:

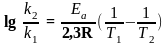чи

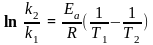
За цими рівняннями можна розрахувати відношення констант швидкості реакції при двох температурах, якщо відома Е_а, чи енергію активації Е_а, якщо відоме співвідношення констант швидкостей реакції при двох температурах.

Аналогічне рівняння можна вивести із швидкостей реакції:

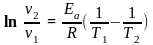
Якщо ∆T = 10, то k₂/k₁ = γ і тоді:

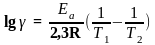
Розрахунки показують, що при γ = 2-4 і при T = 300K Е_a = 57-114 кДж/моль, а для температури 500 К Е_а = 236-472 кДж/моль.

Необхідність введення стеричного множника пояснюється тим, що співудари навіть між активними молекулами приводять до проходження реакції не завжди, а лише при певній орієнтації молекул. Також сильно впливає участь складних по структурі молекул, де число сприятливих для протікання реакції орієнтацій досить обмежене.

Приклад. Енергія активації деякої реакції дорівнює 76 кДж/моль і при температурі 27 ^оС протікає зі швидкістю k₁. За наявності каталізатора при цій же температурі швидкість реакції зростає у 3,38∙10⁴ разів. Визначте енергію активації реакції за наявності каталізатора.

Розв’язання

Константа швидкості без каталізатора рівна:

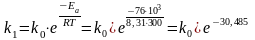
Із каталізатором константа швидкості рівна:

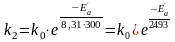
За умовою задачі:

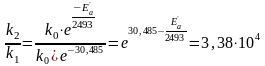
Звідки:

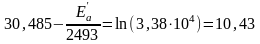
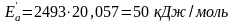
Залежність швидкості хімічної реакції від температури можна виразити у вигляді емпіричного правила Вант-Гоффа: підвищення температури на кожні 10 градусів збільшує швидкість реакції приблизно в 2—4 рази.

У математичній формі правило Вант-Гоффа записується так:

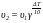(6.3)

де ΔT – збільшення температури;

υ₁ – швидкість реакції до підвищення температури;

υ₂ – швидкість реакції після підвищення температури (від температури Т₁ до температури Т₂);

γ – температурний коефіцієнт швидкості реакції (γ = 2...4).

Приклад 4. Температурний коефіцієнт швидкості реакції рівний 2,8. У скільки разів зросте швидкість реакції при підвищенні температури від 20 до 70 ^оС ?

Розв’зок. Позначимо швидкість реакції при 20 і 70 ^оС відповідно через υ₁ і υ₂. Тоді можна записати:

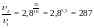
Швидкість реакції збільшиться у 287 разів.

Рівняння Вант-Гоффа є приблизним, оскільки швидкість реакції, крім температури, залежить також від енергії активації ΔE_aкт, яка, в свою чергу, залежить від температури.

Величина енергії активації залежить від природи реагуючих речовин, тому кожна хімічна реакція характеризується своїм значенням Е_акт. У відповідності з рівнянням Арреніуса, чим більша Е_акт, тим важчий перебіг реакції і тим значніший вплив температури на її швидкість. Так, реакції між валентнонасиченими молекулами (прості реакції) потребують високої енергії активації (150 – 450 кДж/моль). Це означає, що більша частина зіткнень взаємодіючих частинок не призводить до перебігу хімічної реакції. Швидкість подібних реакцій досить мала, тому реакції між валентнонасиченими молекулами трапляються рідко. Навпаки, незначна енергія активації реакції свідчить про те, що більша частина зіткнень між частинками реагуючих речовин призводить до хімічної взаємодії. Такі реакції перебігають практично миттєво. Прикладом реакцій з малою величиною енергії активації можуть бути реакції між йонами протилежного знаку (0 – 80 кДж/моль) або між вільними радикалами (0 – 40 кДж/моль).

Зменшити енергію активації системи можна іншими шляхами: дією випромінювання (ультрафіолетового, рентгенівського, γ-випромінювання) або електричним розрядом.