Элементарные геометрические соображения позволяют записать такое преобразование в виде:

Таким образом, поворот задается матрицей: . Следовательно, имеет место преобразование:

.

Аналогично, в случае трехмерного пространства поворот, например, относительно оси Oy на угол v будет задаваться матрицей:

, .

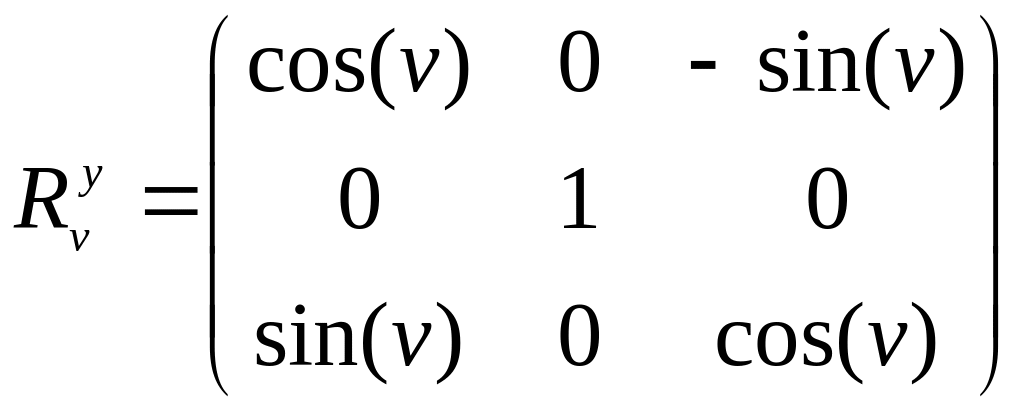Сжатие – растяжение. В случае изменения масштаба вдоль оси Ox, все объекты пространства преобразуются по правилу: . Если при этом k>1, то преобразование является растяжением. Если 0<k<1, то – сжатием. Такие преобразования даются матрицей: . Аналогично задаются сжатия-растяжения вдоль осей Oy и Oz.

Однородные координаты и перенос. Для сохранения универсальности описания преобразований пространства используется идея введения однородных координат. Дело в том, что основная операция – параллельный перенос на вектор , не может быть описан матрицами размера 33.

Пусть объект трехмерного пространства задан координатами . Предположим, что он является элементом пространства большей размерности и лежит на декартовой гиперплоскости , где h – координата четвертого измерения. Рассмотрим координатную прямую, которая проходит через точку параллельно оси Oh. На ней находится бесконечно много (континуум) копий исходной точки. Среди них выберем точку, находящуюся на «высоте» h. Очевидно, что она имеет координаты . Их и называют однородными. Вообще, однородные координаты задают некую виртуальную копию нашего исходного трехмерного пространства. И таких копий бесконечно много. В принципе, из них можно брать любую. Выбор h=1 – это вопрос выбора масштаба вдоль четвертой координаты.

Теперь задача преобразования пространства на вектор параллельного переноса может быть описана при помощи матриц размерности 44. Пусть, например, надо описать перенос вдоль оси Ox на величину a:

.

Очевидно (следуя правилам умножения матрицы на вектор), что такое преобразование может быть записано в виде:

,

где .

Заметим, при описании преобразований поворота и сжатия-растяжения четвертая (однородная) координата не преобразуется, следовательно, в последней строке матрицы преобразования должна стоять единица, тогда как все остальные её элементы являются нулями.

Таким образом, мы описали все основные преобразования пространства.

Аффинные преобразование и их свойства. Все рассмотренные выше преобразования были невырожденными (определители их матриц не равны нулю). Следовательно, вместе с ними могут быть определены обратные преобразования – повороты, переносы, растяжения-сжатия, при помощи которых элементы пространства «возвращаются» в свое исходное состояние. Такие преобразования называются аффинными.

Преобразование пространства с однородными координатами может быть описано матрицей общего вида:

, .

Мы будем рассматривать такие преобразования, которые сохраняют взаимно однозначные соответствия объектов и ; их главный определитель . Рассмотрим их основные свойства.

1. Если – аффинное преобразование, то – также аффинное преобразование (обратное преобразование является аффинным).

2. Если , – аффинные преобразования, то – аффинное преобразование (суперпозиция аффинных преобразований является аффинным).

3. Существует тождественное (единичное) аффинное преобразование:

.

Ортогональные преобразования. Среди аффинных преобразований можно выделить важный класс преобразований, сохраняющих длину вектора. Такие преобразования называются ортогональными. К ним относятся повороты, перенос и любые их суперпозиции. Для них выполняются все свойства аффинных преобразований. Кроме того, они, вместе с длиной вектора, сохраняют еще и величины углов преобразуемых объектов (это свойство является следствием теоремы косинусов), в том числе – свойства параллельности и ортогональности. Тем самым, ортогональные преобразования полностью сохраняют начальную форму объекта и их взаимное расположение на сцене.

Если преобразование задано матрицей, то критерием его ортогональности является следующие условия:

Инвариант аффинного преобразования. Величина, сохраняемая при преобразовании пространства, называется инвариантом преобразования. Инвариантом произвольного аффинного преобразования является простое отношение: , где C – внутренняя точка интервала . В результате аффинного преобразования отрезок перейдет в отрезок , а точка – в точку , при этом .

Основным свойством инвариантности аффинного преобразования относительно простого отношение является сохранение вида кривых и поверхностей второго порядка: эллипсы и эллипсоиды переходят в эллипсы и эллипсоиды, параболы и параболоиды – в параболы и параболоиды, гиперболы и гиперболоиды – в гиперболы и гиперболоиды.

Вопросы для самоконтроля.

Вопрос 1. Как записать матрицы поворота вокруг осей Ox и Oz?

Вопрос 2. Чему равен определитель матрицы:

а.) поворота?

б.) сжатия с коэффициентом k?

в.) переноса?

Вопрос 3. Как выглядит матрица переноса на вектор ?

Вопрос 4. Что произойдет с точкой пересечения медиан треугольника (его геометрическим центром) при аффинном преобразовании?

Задачи.

Задание 1. Объясните, почему в результате аффинного преобразования прямые переходят в прямые.

Указание: рассмотрите матричную форму преобразования и учтите, что оно не вырожденно.

Задание 2. Постройте составную матрицу поворота на угол  вокруг оси Oz и переноса на вектор .

Задание 3. Постройте составную матрицу растяжения вдоль оси Ox переноса на вектор .

Задание 4. Найдите матрицы всех обратных преобразований.