Численное моделирование плоского и осесимметричного течений при внезапном изменении сечения потока

1. Цель работы

Целью работы является изучение течения при внезапном расширении или сужении потока газа. Методом исследования является численное моделирование в двумерной постановке.

2. Основы теории

В проекциях на оси цилиндрической системы уравнения течения газа в рассматриваемых объектах в осесимметричной постановке имеют вид:

- уравнение неразрывности

, (1)

- уравнения импульса

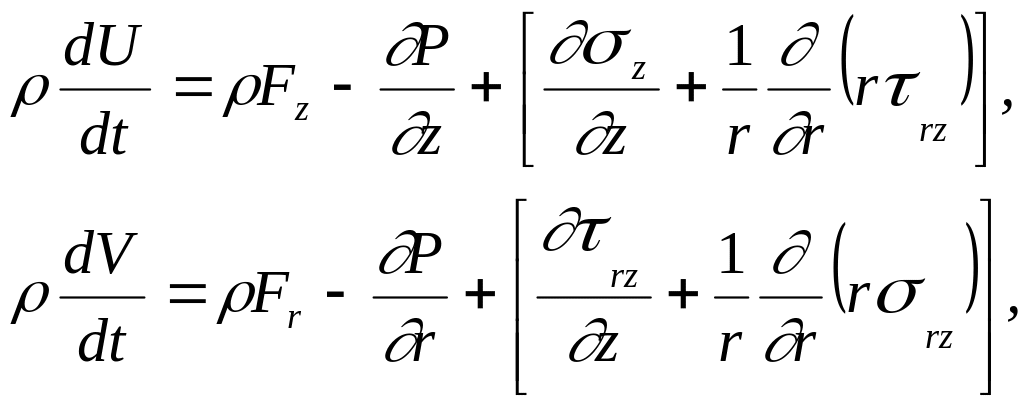(2)

- уравнение энергии

₍₃₎

где U, V – составляющие скорости по осям z и r соответственно; формулы для напряжений вязкости имеют вид:

₍₄₎

На непроницаемой стенке граничные условия имеют вид: u = 0, v = 0.

На оси симметрии должно быть задано условие : v = 0.

Блок-схема алгоритма численного моделирования указанного процесса методом крупных частиц имеет вид.

Рис. 1. Блок-схема алгоритма.

При расчетах особое внимание уделяется сходимости и устойчивости решения. Используемая разностная схема является многослойной, а ее разностные уравнения - это нелинейные уравнения с переменными коэффициентами. Строгий анализ устойчивости такой схемы затруднителен. Для оценки устойчивости используются приближенные соотношения

где С - коэффициент у дивергентных членов в дифференциальных уравнениях переноса (скорость конвекции),  - коэффициент у диссипативных членов (коэффициент диффузии), x и t - шаги по пространственной координате и по времени. Учитывая, что в рассмотренных конечно-разностных уравнениях применялась аппроксимация первого порядка точности, обеспечивающая устойчивый расчет без введения искусственной вязкости, в качестве оценки устойчивости можно использовать простейшую формулу Куранта t  x/a², где x - минимальный линейный размер частицы, a² - местная скорость звука. Получаемый по указанным условиям шаг t для рассматриваемых течений составляет величину порядка 10^-6 ... 10^-7 с., что существенно меньше величины, обеспечивающей сходимость решения.

Размеры конечных частиц также не могут задаваться произвольно, т.к. они определяют точность приближенного численного решения. Конечная величина пространственных размеров частиц определяет возникновение схемной вязкости, пропорциональной линейному размеру частиц, местной скорости и ее градиенту. Практически это проявляется лишь в зонах больших градиентов: у поверхности тел, в зонах срыва потока и т.п.. Это приводит к "размазыванию" пограничного слоя на несколько ячеек. Однако, важным свойством схемной вязкости метода крупных частиц является то, что она не нарушает характера решения исходного дифференциального уравнения. В областях же гладкого течения, где градиенты параметров потока сравнительно малы, влияние схемной вязкости незначительно.