Вступ  

       Якщо тіло рухається або має тенденцію до руху по поверхні другого тіла, виникає сила опору, яка створюється в зоні контакту між поверхнями тіл. Ця сила називається фрикціонною силою або просто силою тертя.  Максимальна величина сили тертя, при якій рух тіла стає неминучим, називається граничним тертям.  Експериментально знайдено, що модуль сили граничного тертя пов’язано з відношенням цієї сили до нормальної реакції між двома поверхнями. Це відношення є сталою величиною і називається коефіцієнтом тертя.   Тертя розділяється на зовнішнє і внутрішнє.  Тертя зовнішнє,  це є механічний опір, що виникає в площині дотикання двох тіл при відносному переміщенні одного з них по поверхні другого.  Тертя внутрішнє, це є сукупність різноманітних процесів, що відбуваються у внутрішньому об’ємі твердого тіла (а також в рідинах і газах) і призводять до необерненого розсіяння механічної енергії при деформації, що зв’язана з перетворенням механічної енергії у теплову.

       Розглянемо тертя зовнішнє, враховуючи, що в курсі теоретичної механіки тіла вважаються абсолютно твердими і тому внутрішнє тертя теоретично не відбувається. Головні означення

Статичне тертя проміж двома тілами є дотична сила, що чинить опір проковзанню одного тіла по відношенню до другого.  Граничне тертя є максимальна величина сили статичного тертя, коли рух становиться неминучим.  Кінетичне тертя є дотична сила між двома тілами після початку руху. Ця сила менше, ніж статичне тертя.  Кут тертя є кут між лінією дії реакції, що виникає при дії одного тіла на друге, і нормаллю до дотичної площини між тілами, коли рух становиться неминучим.  Коефіцієнт статичного тертя   є відношення сили граничного тертя   до нормальної реакції  :  . Коефіцієнт кінетичного тертя є відношення сили кінетичного тертя до нормальної реакції між тілами.  Граничний кут нахилу площини   є кут, на який нахилена площина може бути повернена до того, як об’єкт, що знаходиться на ній, не почне рухатись під дією сили тяжіння і реакції площини (Рис. 1).

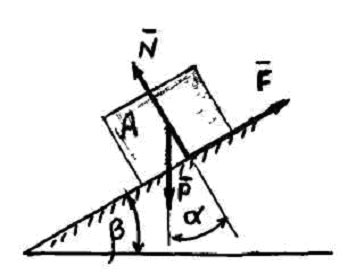
Рис. 1

Хоча рух буде неминучим при подальшому найменшому збільшенні кута  , тіло   знаходиться ще у рівновазі. Оскільки  , коефіцієнт тертя може виражатися кутом підйому площини на кут  , при якому рух становиться неминучим. При цьому куті   і тому можна записати, що  .

Закони тертя

Сила тертя завжди спрямована протилежно до напряму руху тіла.  

 Коефіцієнт тертя не залежить від площі контакту між тілами. 

Коефіцієнт кінетичного тертя менше в порівнянні з коефіцієнтом статичного тертя.

Тертя не залежить від швидкості переміщення одного тіла по поверхні другого, але при великих швидкостях відмічається зменшення сили тертя.

Сила статичного тертя не може бути більше, ніж необхідно, щоб утримувати тіло у рівновазі. При розв’язку задач, де розглядається статичне тертя, необхідно враховувати, що сила тертя є незалежна і невідома величина, доки положення тіла не становиться таким, що його рух є неминучим. У цьому разі можна використовувати силу граничного тертя

.

Кут тертя; конус тертя

1)Кут тертя.  Припустимо, що блок, показаний на Рис. 2а, знаходиться під дією сили  . Нехай   є фрикціонна сила, що виникає внаслідок дії сили  , і   - нормальна реакція. Таким чином, в контактній поверхні реакціями до тіла є   і  . Складемо їх геометрично і одержимо реакцію  , що діє під кутом   до нормальної реакції. Звідси кут  , що зветься кутом тертя, дорівнює: 

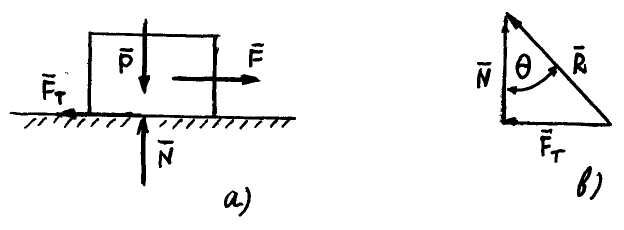
Рис. 2

В той час як фрикціонна сила збільшується, збільшується і кут  . Цей кут може досягти максимума, коли гранична величина тертя досягнута. В цьому разі, якщо позначимо  :    Величина   називається кут граничного тертя. Звідси, кут граничного тертя може бути визначеним як кут проміж рівнодійною реакцією і нормаллю до поверхні, по якій рух тіла становиться неминучим.

2)  Конус тертя.  Коли тіло досягає стану неминучого руху в напрямі сили  , сила тертя стає граничною і результуюча сила реакції стає також граничною. При цьому вона спрямована під кутом   до нормальної реакції. Якщо тіло має стан неминучого руху в інших напрямах, реакція   також становиться граничною. Таким чином, коли напрям сили   поступово міняється на  , рівнодійна реакції  , як твірна, описує конус з центральним кутом   (Рис. 3).

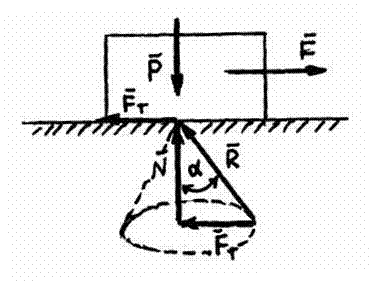
Рис. 3

Якщо результуюча реакція знаходиться на поверхні конуса тертя, рух тіла становиться неминучим. Якщо результуюча реакція знаходиться в середині конуса тертя, тіло знаходиться у рівновазі. Цей конус носить назву конус тертя.

Тертя кочення

Тертя кочення має місце при котінні катка по не абсолютно твердій поверхні. Під дією сили тяжіння катка виникає деформація поверхні, що призводить до виникнення опору котінню катка.  Розглянемо приклад.  Колесо (каток) вагою   і радіуса   котиться по горизонтальній площині під дією сили  , що прикладена до центра колеса (Рис. 4).

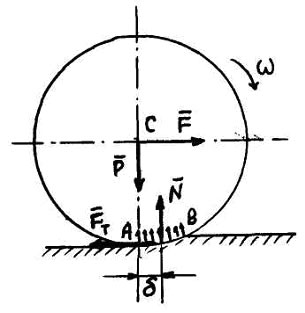
Рис. 4

В результаті у напрямі руху катка створюється участок   поверхні, в кожній точці якої виникає відповідна сила опору руху катка, тобто створюється розподілена по   система сил. Розкладаючи ці сили на вертикальну і горизонтальну складові, бачимо, що вертикальна складова   зміщена по відношенню до вертикального діаметра катка на відстань  . Ця відстань називається коефіцієнтом тертя кочення і являє собою плече пари сил ( ,  ), дія якої протилежна по відношенню до напряму руху катка.  Момент пари сил ( ,  ) дорівнює   і називається моментом пари сил тертя кочення.  Горизонтальна складова опорної реакції дорівнює   і називається силою опору кочення.  Відмітимо, що величини коефіцієнта тертя кочення для різних матеріалів приводяться в таблицях.

Задача1: Драбина   довжиною 12 метрів важить  . Вона приставлена до вертикальної стіни і знаходиться на горизонтальній підлозі, як показано на Рис. 10(а). Чому має дорівнювати коефіцієнт тертя   для рівноваги?

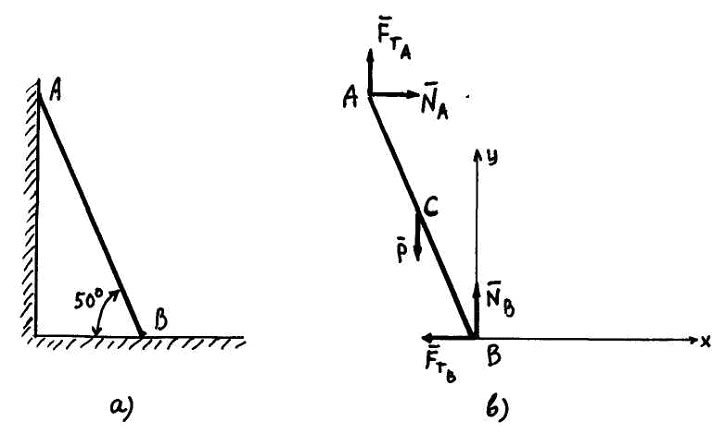
Рис. 10  

       Розв’язок  Об’єкт рівноваги показано на Рис. 10(б). До нього прикладена   в центрі драбини, а також реакції в т.   і  . В цих точках прикладені граничні величини сил тертя   і  .   і  . Складемо рівняння рівноваги для драбини  :  1)  ;  2)  ;  3)  .  Підставляючи значення   з першого рівняння в друге, знаходимо:  .  Використовуючи знайдене значення   в третьому рівнянні, одержуємо:  .  Звідки маємо:  .

Задача2: Визначити найменший кут   для рівноваги однорідної драбини довжиною  , що спирається на стіну. Коефіцієнт тертя для всіх поверхонь  .

Розв’язок Вважаючи проковзання неминучим, накреслимо об’єкт рівноваги (Рис. 11)

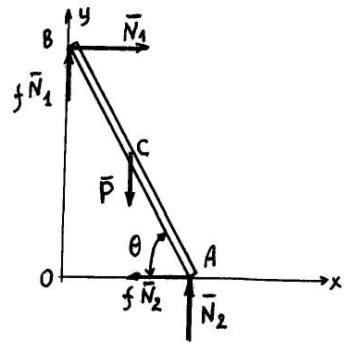
Рис. 11

       Складемо три рівняння рівноваги:

1)  ;  2)  ;  3)  .  Підставляючи   в друге рівняння, одержимо:  .  Підставивши значення   в третє рівняння, маємо:  . Це є критичне значення кута  , при якому драбина залишається у рівновазі.

Задача3: Визначити величину сили  , яка необхідна для того, щоб привести в рух блок масою  . Коефіцієнт статичного тертя між блоком і горизонтальною поверхнею дорівнює   (Рис. 12).

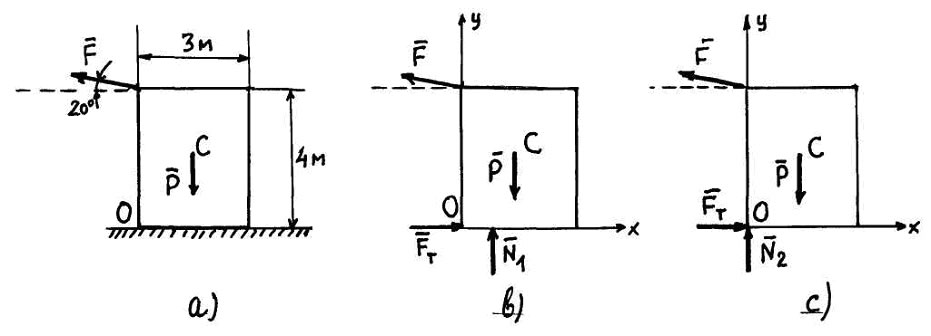
Рис. 12

Розв’язок Рух блока можливий у двох випадках. Блок може ковзати ліворуч або повертатися навколо т. О (Рис. 12 (a)). Спочатку визначимо величину ваги блока. Вона дорівнює:  . Розглянемо варіант, коли блок почне рухатись поступально, тобто без поворотів навколо т. О. В цьому випадку гранична величина тертя має місце, як це показано на Рис. 12 (b).  Рівняння рівноваги мають вигляд:  1)  ;                                (1) 2)  .                              (2)   Оскільки  , то після підстановки   у рівняння (2) одержимо:  1)  ;  2)  . Звідси  . Розглянемо Рис. 12 (с). Припустимо, що блок повертається навколо т. О. Визначимо величину сили   для даного випадку. Звернемо увагу на те, що в цьому разі не дається величина сили тертя. Позначимо її  , як вказано на Рис. 12 (с). При повороті блока він контактує з поверхнею в т. О,де і прикладена реакція  . Рівняння рівноваги записується так:  1)  ;  2)  ;  3)  .  З третього рівняння  . Аналіз задачі можна на цьому закінчити того, що при ковзані сила  , тобто значно менше.  Звідси видно, що при дії сили   блок буде рухатись вздовж площини.

Задача4: Які горизонтальні сили   треба прикласти до блоків   і  , щоб підняти вантаж   вагою  . (Рис. 13 (a)). Коефіцієнт тертя ковзання між блоками   і   і поверхнею дорівнює  , а між блоками   і   і вантажем    . Врахувати симетричність конструкції.

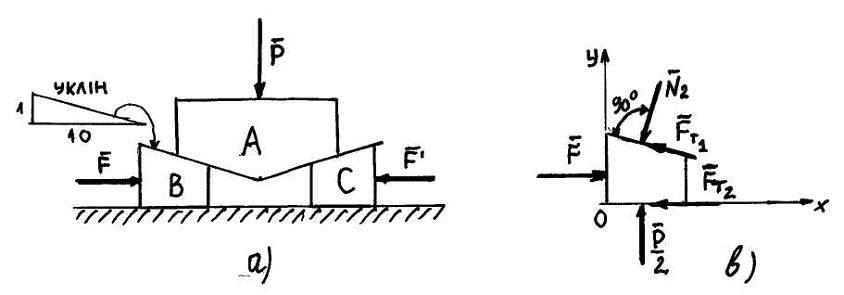
Рис. 13

Розв’язок Розглянемо блок   як об’єкт рівноваги. Сила тертя   спрямована протилежно до сили  . Модуль цієї сили дорівнює  . Модуль сили  . Рівняння рівноваги блока   записується так (Рис. 13 (b)):  1)  ;  2)  .  З рівняння (2),  . Підставивши в рівняння (1), одержимо  .

 Задача5: Чи буде блок вагою   (Рис. 14 (а)) утримуватись у рівновазі горизонтальною силою  . Коефіцієнт статичного тертя  .

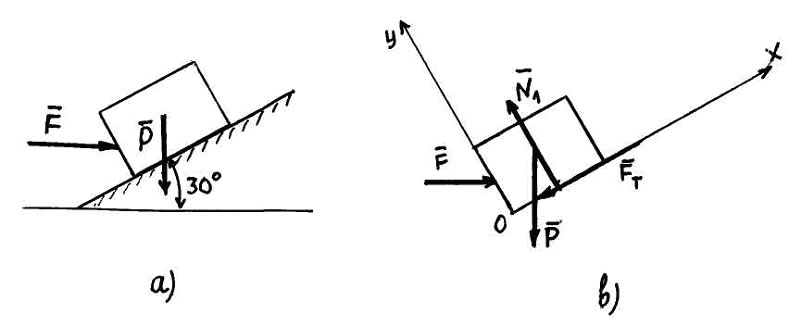
Розв’язок  В цьому випадку треба враховувати, що сила тертя повинна бути менше ніж критична її величина. Припустимо, що сила   є цілком достатньою для утримання блока від ковзання по нахиленій площині. Тоді вона може бути достатньою, щоб спричинити рух блока вгору по площині. Враховуючи цю умову, покажемо, що сила тертя   діє донизу вздовж площини, як вказано на Рис. 14 (b).  Рівняння рівноваги блока в проекціях на осі, що паралельні і перпендикулярні до площини, записуються так:  1)  ;  2)  .

Розв’язуючи ці рівняння, одержимо:  . Це показує, що величина сили  , яка необхідна для утримання блока у рівновазі, дорівнює  . При цьому, максимальна величина цієї сили обмежена  . Це означає, що блок буде рухатись вздовж площини вгору.

Задача7: Чому має дорівнювати кут   з тим, щоб рух блока   масою   у напряму донизу вздовж площини був неминучим? Коефіцієнт тертя на всіх поверхнях   (Рис. 16 (a)). Маса блока   дорівнює  .

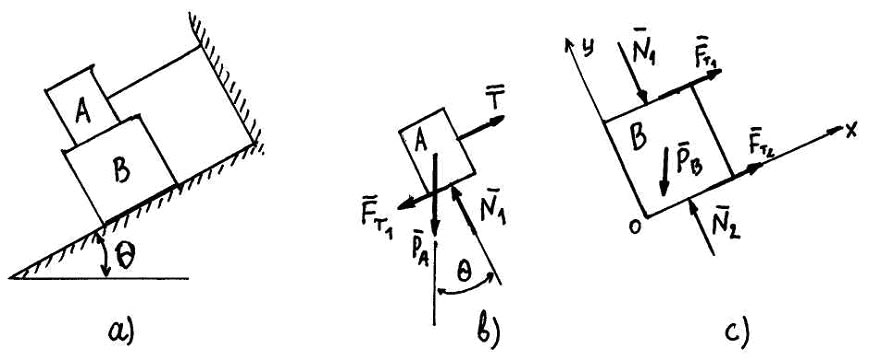
Рис. 16  

Розв’язок  Покажемо об’єкти рівноваги двох блоків і складемо суми проекцій сил на осі   і  . Вісь   паралельна до площини, вісь   - перпендикулярна.  ,      . З схеми (b) видно, що  . Рівняння рівноваги для блока   запишуться так:  1)  ;  2)  .  Підставляючи   в перше і друге рівняння, знаходимо, що  .

Задача8: Тіло вагою   знаходиться в стані спокою на площині, нахиленій під кутом   до горизонталі, як показано на Рис. 17. Кут статичного тертя між тілом і площиною дорівнює  . Яку горизонтальну силу   треба прикласти до тіла, щоб утримувати тіло від проковзання по площині?

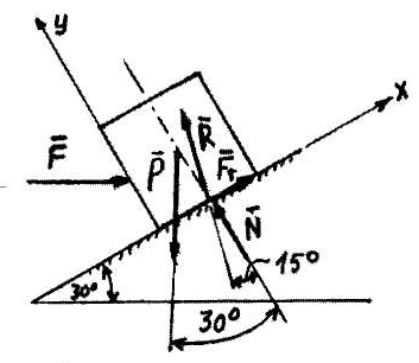
Задача9: Визначити силу  , що необхідна для приведення в рух системи двох блоків вагою :  . Сила   паралельна до нахиленої площини. Прийняти, що коефіцієнт тертя ковзання  . Блок невагомий (Рис. 18 (a)).

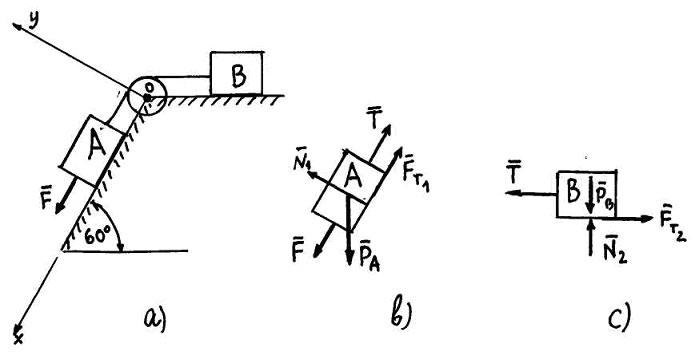
Рис. 18  

Розв’язок  Накреслимо об’єкти рівноваги блоків   і   (Рис. 18 (b) і (c)).   - натяг нитки, що з’єднує блоки. З аналізу  . Також,  , звідси  .  Сума проекцій сил на вісь  , що паралельна до нахиленої площини:

, звідси  .