12. Алгебраическая форма записи комплексного числа.

Обозначим через z=(a,b)∈ℂ - произвольное комплексное число. Можно представить z в виде z=(a,b) (a,0)+(0,b) (a,0)+(b,0)⋅(0,1) a+bi.

Определение 1. Алгебраической формой записи комплексного числа называется представление комплексного числа z=(a,b) в виде z=a+bi, где a,b∈ℝ, i²=-1.

При этом а называется действительной частью комплексного числа z, и обозначается a=Re z, b – мнимой частью комплексного числа z и обозначается b=Im z.

Операции над комплексными числами в алгебраической форме.

Пусть z₁=a+bi, z₂=c+di

1. Сложение z₁+z₂=(a+c)+(b+d)i.

2. Умножение z_1⋅z₂=(ac-bd)+(ad+bc)i.

Правила сложения и умножения комплексных чисел в алгебраической форме следуют непосредственно из правил (1) и (2) в определении 2 §11.

Определение 2. Комплексно сопряженным с числом z=a+bi∈ℂ называется число =a-bi∈ℂ.

3. Деление = = = =

4. Извлечение квадратного корня. Пусть z=a+bi, найдем .

Пусть =x+yi z=(x+yi)², т.е. a+bi=(x²-y²)+2xyi 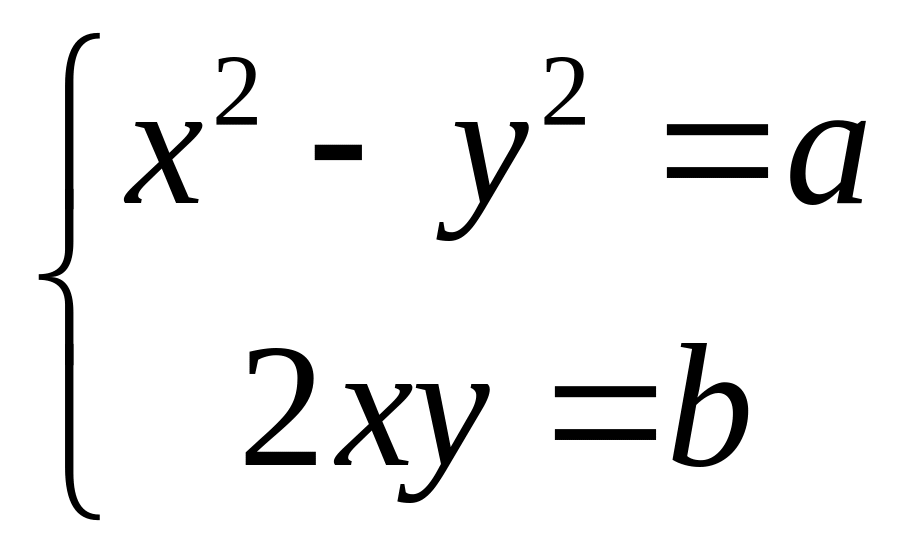. Таким образом нахождение сводится к решению системы уравнений .

13. Тригонометрическая форма записи комплексного числа

Каждому комплексному числу z соответствует на плоскости в декартовой системе координат точка с координатой (а; b). Верно и обратное. Каждой точке на плоскости в декартовой системе координат соответствует упорядоченная пара действительных чисел, то есть соответствует некоторое комплексное число. Таким образом, между множеством ℂ и множеством всех точек плоскости существует взаимно-однозначное соответствие, это означает, что мы можем считать, что каждое комплексное число изображается точкой на плоскости. Поэтому, плоскость также называют комплексной плоскостью.

Пусть z=(а; b)=а+bi. Изобразим число z на плоскости.

b

M(a;b)

r



a

O

Любая точка на плоскости может определяться не только своими декартовыми координатами, но и координатами, которые называются полярными: М(r,), где r=ОМ,  – угол между Ox и ОМ.

Таким образом, каждое комплексное число должно однозначно определяться своими полярными координатами r и .

Определение 1. Модулем комплексного числа z= а+bi называется длина радиус вектора точки М(а;b). И обозначается |z|=r.

Из ОАМ r = (1)

Определение 2. Аргументом комплексного числа z=a +bi называется угол  между положительным направлением оси Ox и радиус-вектором ОМ точки М(а;b) и обозначается arg z=.

Аргумент комплексного числа определяется не однозначно, а с точностью до 2. Значение аргумента, принадлежащее интервалу [0;2) называется главным значением аргумента и обозначается Arg z.

аrg z=Arg z+2 k , k∈ℤ.

Из ОАМ: 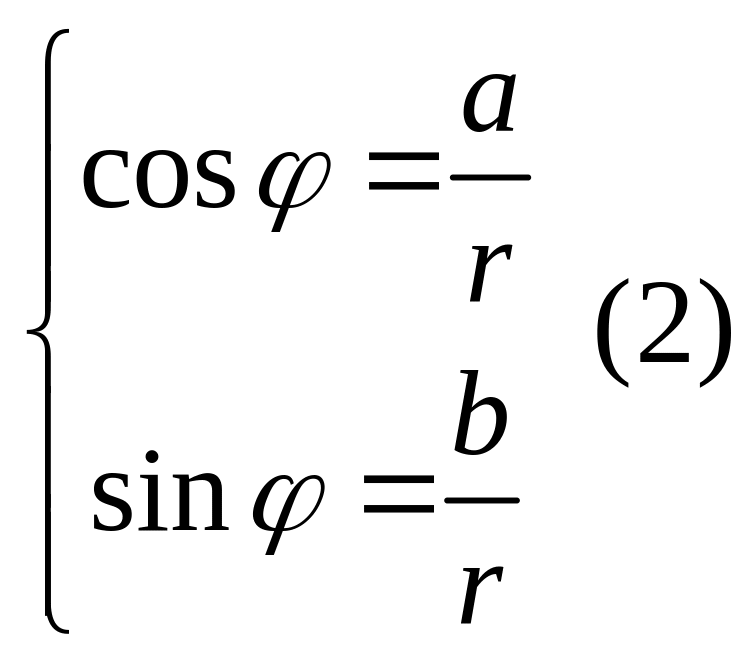, тогда .

Таким образом, z=a+bi = r⋅сos +r⋅sin⋅i = r(cos +i⋅sin)

Определение 3. Запись z= r(cos +i⋅sin) , где r = и называется тригонометрической формой записи комплексного числа z=a+bi.

Замечание Для комплексного числа 0 , модуль равен нулю, а аргумент не определяется. Поэтому тригонометрической формой числа 0 является следующая запись: 0=0⋅(cos +i⋅sin), где  - произвольный угол.

Операции над комплексными числами в тригонометрической форме

Пусть z₁ =r₁⋅(cos ₁+i⋅sin ₁), z₂ =r₂⋅(cos ₂+i⋅sin ₂).

1. Умножение z₁z₂= r₁ r₂⋅(cos ₁+i⋅sin ₁)⋅(cos ₂+i⋅sin ₂)= =r₁r₂ ((cos ₁ ⋅cos ₂ –sin₁ ⋅sin₂ ) + i(sin ₁⋅cos₂ + sin ₂ ⋅cos ₁)) = =r₁r₂ (cos(₁ +₂)+i⋅sin (₁ +₂ )).

Таким образом, z₁z₂ = r₁r₂ (cos(₁ +₂)+i⋅sin (₁ +₂ )), т.е. при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются.

2. Деление. Пусть z₁ =r₁⋅(cos ₁+i⋅sin ₁), z₂ =r₂⋅(cos ₂+i⋅sin ₂), причем z₂0.

= (cos(₁ -₂)+i⋅sin (₁ -₂ ))

Таким образом, (cos(₁ -₂)+i⋅sin (₁ -₂ )), т.е.при делении комплексных чисел в тригонометрической форме, их модули делятся друг на друга, а аргументы вычитаются.

3. Возведение в степень. Пусть z= r⋅(cos +i⋅sin ) Тогда, по правилу умножения комплексных чисел, z²=z⋅z=r²(сos2+i⋅sin2) и т.д. Методом математической индукции можно доказать, что

zⁿ=rⁿ (cos n+i⋅sin n), n∈ℕ, (3)

т.е. при возведении комплексного числа в натуральную степень n, его модуль возводится в степень n, а аргумент умножается на n.

Определение 4. Корнем n-й степени из комплексного числа z называется такое комплексное число u, что uⁿ =z , и обозначается =u_.

4. Извлечение корня n-й степени из комплексного числа z= r⋅(cos +i⋅sin ), z .

Будем искать u в тригонометрической форме, т.е. u=r₀(cos ₀+i⋅sin₀) такое, что uⁿ =z, т.е. (r₀(cos ₀+i⋅sin₀)) ⁿ = r⋅(cos +i⋅sin ). Согласно правилу возведения в степень, получим r₀ⁿ(cos n₀+i⋅sin n₀)= r⋅(cos +i⋅sin ).

Так как равные комплексные числа изображаются одной и той же точкой на плоскости, то из рисунка и определений 1 и 2 следует, что их модули должны быть равны, а аргументы могут отличаться лишь на 2k, k∈ℤ.

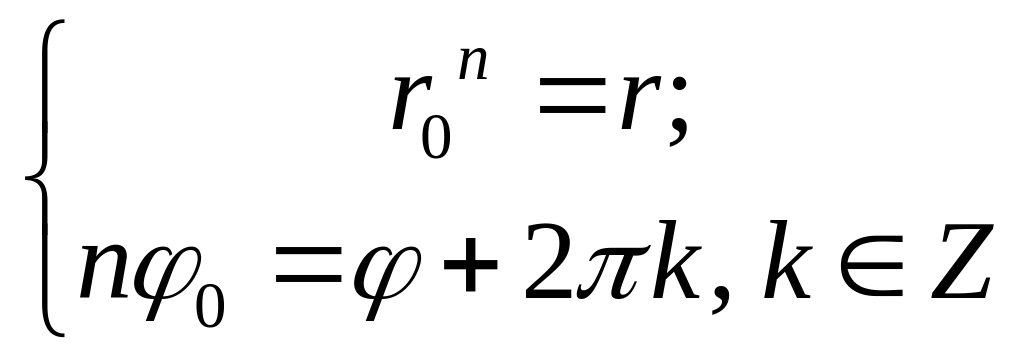, следовательно,

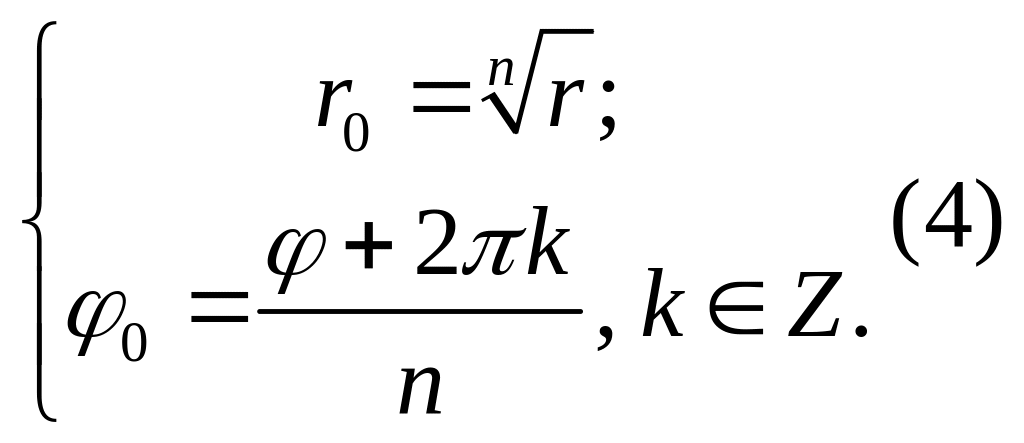
При k=0 ₀₁ =

При k=1 ₀₂ =

При k=2 ₀₃ =

_***

При k=n-1 _0(n-1) = +2 -

При k=n _0n = = +2 = ₀₁

При k=n+1 _0(n+1) = +2 + = ₀₂ и т. д.

Таким образом,

= (cos +i⋅sin ), k= (5)

Корень n-й степени из комплексного числа z имеет n значений z₀,z₁,z₂,…,z_n-1 которые на комплексной плоскости располагаются на окружности радиуса R= и делят окружность на n равных частей.

16