5.2. Определение опорных реакций.

Так как длины всех панелей одинаковы и нагрузка симметрична относительно оси, проходящей через середину фермы, реакции правой и левой опор будут равны и составляют:

V_A = V_B = (ΣFi + ΣT_P)/2 = (8F + 2T_P)/2 = 4F+T_P = 4∙23,16+107,7 =  200 кН

5.3. Расчёт усилий в стержнях фермы

Дальнейший расчёт ведём комбинацией метода «вырезания узлов» и метода «сечений (метод моментной точки)». Все неизвестные усилия в вырезанных узлах и отсечённых частях фермы считаем положительными (растяжение) и направленными от узла наружу.

На рис.3 представлена ферма со всеми действующими активными и реактивными усилиями, сечениями ивырезанными узлами.

Рис.4. Схема фермы с указанием сечений и вырезаемых узлов

5.3.1. Вырезаем узел А (рис.4 и рис.5) и рассматриваем его равновесие в проекциях сил на оси координат.

ΣX=0; N_А-2 =0;

ΣY=0; V_A + N_A-1 =0; откуда N_A-1= - V_A = -200  кН

N_А-2 =0; N_А-1 = -200 кН

Рис.5. Узел А

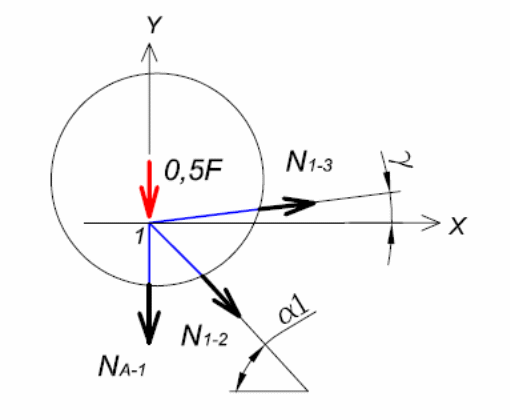
5.3.2. Вырезаем узел 1 (рис.4) и рассматриваем его равновесие в проекциях сил на оси координат.

ΣY=0; - N_A-1 - 0,5F +N_1-3∙ sin γ - N_1-2∙sin α₁=0; откуда

N_{1-3 =} ( N_1-2 ∙ sin α₁ + N_A-1 + 0,5F)/ sin γ =

[N_1-2 ∙ sin 45,22° + (- 200) + 0,5∙23.16]/ sin 7,125° = (N_1-2 ∙ 0,7098 – 188.42)/0,1240, или

N_1-3 = 5,724∙ N_1-2 -1520 (1)

ΣX=0; N_1-3∙cos γ + N_1-2 ∙ cos α₁ = 0, откуда N_1-3= -N_1-2∙cos α₁ / cos γ =

-N_1-2∙cos 45,22° / cos 7,125° =

-0,7099 N_1-2 (2)

Подставив (2) в (1), получим:

-0,7099 N_1-2 = 5,724∙ N_1-2 -1520, или 6,434 N_1-2 = 1520, откуда

N_1-2 = 1520/6,434 = 236,2 кН.

N_1-3 = 5,724∙ N_1-2 -1520 =

5,724∙ 236,2 - 1520 = - 168 кН

N_1-2= 236,2 кН;

N_1-3= -168 кН;

Рис.6. Узел 1.

5.3.3. Проводим сечение I-I

Проводим сечение I-I (см. рис.3 и рис.4).

Сечение проводим таким образом, чтобы линия сечения пересекала не более 3-х стержней с неизвестными усилиями. Рассмотрим равновесие левой отсечённой части относительно узлов, в которых сходятся два стержня с неизвестными усилиями. Моменты всех сил относительно выбранных узлов должны равняться нулю.

Рассмотрим равновесие левой отсечённой части (рис.7).

М омент всех сил относительно узла 2, в котором сходятся линии действия усилий N_2-5 и N_2-4 равен нулю, или:

ΣМ₂=0;

(V_A- 0,5F)∙d∙ cos γ + N_3-5∙ cos γ∙h₂=0; откуда

N_3-5 = [-(V_A-0,5F)∙d]/h₂ = [-(200- 0,5∙23,16)∙2,0]/2,248 = -167,6 кН

Сумма проекций всех сил на ось Y равна нулю: ΣY=0;

V_A - 0,5F - F + N_3-5 ∙ sin γ + N_2-5 ∙ sin α₂ = 0,

откуда:

N_2-5 = (1,5 F - V_A - N_3-5 ∙ sin γ )/ sin α₂ =

Рис. 7. Левая отсечённая часть [1,5∙23,16 - 200 - (- 167,6)∙ sin 7,125°]/

sin 51,55° = - 143,7/0,7832 = -184,5 кН

Сумма проекций всех сил на ось X равна нулю: ΣX=0;

N_3-5 ∙ cos γ + N_2-5 ∙ cos α₂ + N_2-4 = 0;

откуда N_2-4 = - N_3-5 ∙cos γ - N_2-5 ∙cos α₂ = -(-167,6)∙ cos7,125° - (-184,5)∙ cos 51,55° = 281,1 кН

N_3-5 = - 167,6 кН; N_2-5 = - 184,5 кН; N_2-4 = 281,1 кН

5.3.4. Вырезаем узел 4 (рис.4 и рис.8) и рассматриваем его равновесие в проекциях сил на оси координат.

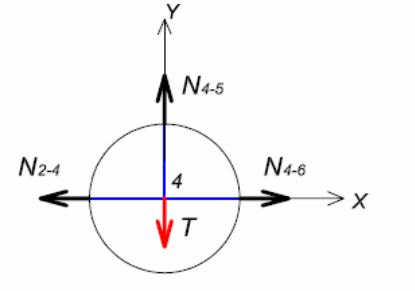
ΣX=0; -N_2-4 + N_4-6 = 0; откуда

N_4-6 = N_2-4 = 281,1 кН

ΣY=0; N_4-5 - Т = 0, откуда N_4-5 = Т =

107,7 кН

N_4-6 = 281,1 кН; N_4-5 = 107,7 кН

Рис. 8. Узел 4.

5 .3.5. Проводим сечение II-II (рис.4 и рис.9). Сечение проводим таким образом, чтобы линия сечения пересекала не более 3-х стержней с неизвестными усилиями. Рассмотрим равновесие левой отсечённой части относительно узлов, в которых сходятся два стержня с неизвестными усилиями. Моменты всех сил относительно выбранных узлов должны равняться нулю

Рис.9. Левая отсечённая часть

ΣМ₆ = 0;

(V_A-0,5F)∙3d∙ cos γ -F∙2d∙cos γ – (F +T) )∙d∙ cos γ + N_5-7 ∙h₃ ∙ cos γ + N_5-7 ∙d ∙ sin γ = 0; откуда

N_5-7 = [-(V_A-0,5F)∙3d∙ cos γ + F∙2d∙cos γ + (F + T)∙d∙cos γ]/(h₃∙cos γ + d ∙ sin γ) =

[-(200,0 – 11,58)∙3 + 23,16·2 + (23,16 + 107,7)]∙2,0∙0,9923/(2,50·cos 7,125º + 2,0∙ sin 7,125º)· =

= (- 565,3 + 46,3 + 130,9)·2·0,9923/(2,481 + 0,248) = - 770/2,729 = - 282,2 кН

Сумма проекций всех сил на ось Y равна нулю:

ΣY=0;

V_A-0,5F – F –F – T + N_5-7 ∙ sin γ – N_5-6 ∙sin α₂ = 0; откуда

N_5-6 = (V_A-0,5F – F –F – T + N_5-7 ∙ sin γ)/ sin α₂ = (V_A -2,5F - T + N_5-7 ∙ sin γ)/sin α₂ =

[(200,0 - 2,5·23,16 – 107,7 + (-182,2)· sin 7,125º]/ sin 51,55º = 15,1 кН.

N_5-7 = - 182,2 кН; N_5-6 = 15,1 кН

5.3.6. Вырезаем узел 7 (рис.4 и рис.10) и рассматриваем его равновесие в проекциях сил на оси координат.

Σ X=0; -N_5-7 ∙ cos γ + N_5-7 ∙ cos γ = 0;

откуда N_5-7 = N_7-9 = - 182,2 кН;

ΣY=0; -N_6-7 –F+ = 0, откуда

N_6-7 = - F = - 23,16кН;

N_6-7 = -23,16 кН; N_5-7 = N_7-9 = -182,2 кН

Рис.10. Узел 7.

5.3.7. Проводим сечение III-III (рис.4 и рис.11). Сечение проводим таким образом, чтобы линия сечения пересекала не более 3-х стержней с неизвестными усилиями.

Рассмотрим равновесие левой отсечённой части.

Рис.11. Сечение III - III. Левая отсечённая часть.

Сумма проекций всех сил на ось Y равна нулю: ΣY=0;

V_A - 3,5F - T + N_7-9 ∙sin γ + N_6-9 ∙sin α₃ = 0, откуда N_6-9 = - (V_A - 3,5F - T + N_7-9 ∙sin γ)/ sin α₃ = -[200,0 - 3,5∙23,16 – 107,7 + (- 182,2)∙ sin 7,125º]/ sin 56,44° = 14,2 кН.

Сумма проекций всех сил на ось X равна нулю: ΣX=0;

N_7-9 ∙ cos γ + N_6-9 ∙ cos α₃ + N_6-8 = 0, откуда N_6-8 = - N_7-9 ∙ cos γ - N_6-9 ∙ cos α₃ =

- (-182,2) ∙ cos 7,125°- 14,2 ∙ cos 56,44° = 172,8 кН

N_6-9 = 14,2 кН; N_6-8 = 172,8 кН.

5 .3.8. Вырезаем узел 8 (см. рис.4 и рис.12) и рассматриваем его равновесие в проекциях сил на оси координат.

ΣY=0; N_8-8* = 0

Рис. 12. Узел 8